[概率论与数理统计]笔记：5.4 假设检验概述

5.4 假设检验概述

假设检验问题的提法

基本概述

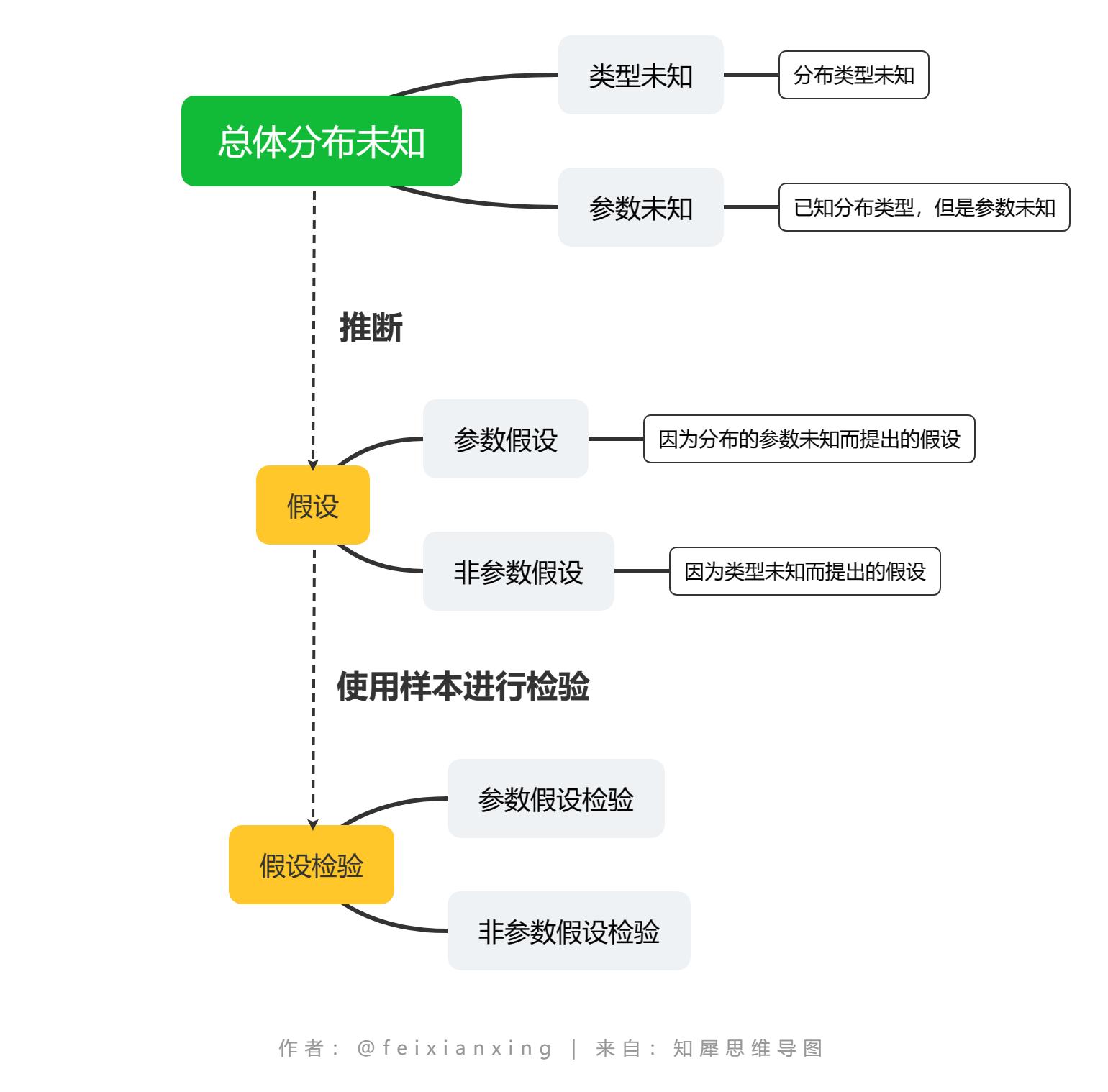
在实际问题中，总体分布通常是未知的，可能是分布的类型未知，也可能是分布的相关参数未知，比如已知是正态分布，但是不知道参数\(\mu,\sigma^2\)是多少。

于是总体分布未知可以分为类型未知 和参数未知 两种情况。

对于这些未知，我们可以提出一种推断，比如说”假设总体服从正态分布“，或者说”假设正态分布的\(\mu\)是100“，这些推断叫做假设 。

因为参数未知进行的推断叫做参数假设 ，而对其他未知比如类型未知进行的推断叫做非参数假设 。

假设之后，我们需要使用样本来证明我们推断的准确性，这个过程叫做假设检验 。

对参数假设进行的检验叫做参数假设检验 ，对非参数假设进行的检验叫做非参数假设检验 。

假设

• 待检验的假设称为原假设 或零假设 ，记作\(H_0\).
• 与之对立的假设称为备择假设 或对立假设 ，记作\(H_1\).

二者是二选一，接受其中一个假设就意味着拒绝另一个假设。

一个假设检验问题通常简记为\(H_0\leftrightarrow H_1\).

案例

有一新工艺，不知道是否能提高生产效率，那么\(H_0\)可以是”生产效率不变”，而\(H_1\)是”新工艺使得生产效率提高“。

\(H_0\)可以理解为研究者想要推翻的结论，\(H_1\)是研究者想要证明的结论。

这个案例可以简记为：\(H_0:生产效率不变\leftrightarrow H_1:生产效率提高\).

假设检验问题

• 显著性假设检验问题——只提出唯一假设\(H_0\)
• \(H_0\)对\(H_1\)假设检验问题——提出两个假设

---

基本思想与原理

小概率原理

小概率事件在一次试验中不太可能发生。

论证逻辑

如果\(H_0\)成立导致了小概率事件发生，那么我们就拒绝假设\(H_0\). (即怀疑该假设的准确性)

基本概念

• 显著性水平\(\alpha\)：在假设检验问题中，小概率事件发生的概率，是事先指定的一个很小的正数。
• 拒绝域：小概率事件对应的样本的取值区域。

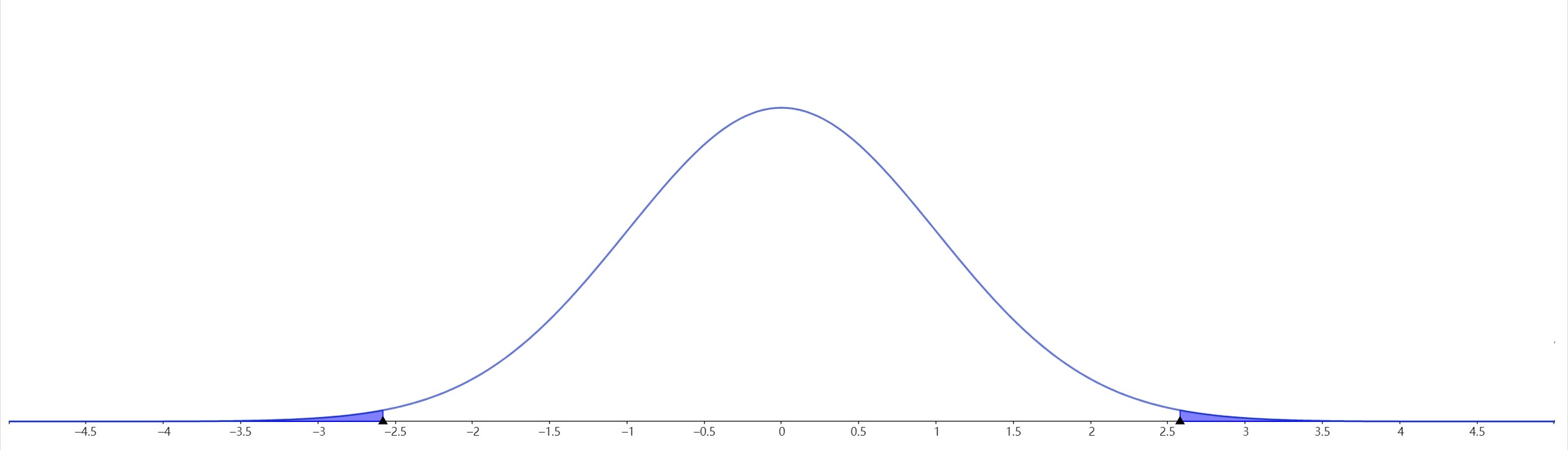
当有样本观察值落在拒绝域 内，就说明发生了小概率事件，于是便拒绝零假设。

假设检验与置信区间

假设检验与置信区间都需要构造枢轴量。

在求解置信区间的时候，枢轴量有一个未知的\(\mu\)或者\(\sigma^2\)需要求解，关注的是概率为\(1-\alpha\)的大概率事件 。

而假设检验的时候，枢轴量中的\(\mu\)或\(\sigma^2\)会代入\(H_0\)假设的数值，然后再根据样本的实际观察值检验是否落在拒绝域内，关注的是概率为\(\alpha\)的小概率事件 。

基本思想

• 构造一个含待检验参数和分布已知的枢轴量\(T\)，在假设\(H_0\)成立的条件下，确定拒绝域。
• 检验法则：小概率事件是否发生。
  • \(P\{(X_1,X_2,\cdots,X_n)\in W\}=\alpha\)对应小概率事件，其中\(W\)称为\(H_0\)的拒绝域 。
  • \(P\{(X_1,X_2,\cdots,X_n)\in \overline{W}\}=1-\alpha\)对应大概率事件，其中\(\overline{W}\)对应\(H_0\)的接受域 。

假设检验的一般步骤

第1步 ：提出\(H_0\leftrightarrow H_1\).

第2步 ：假设\(H_0\)成立，构造枢轴量\(T\)，确定其分布。

第3步 ：对于给定的\(\alpha\)，根据\(P\{(X_1,X_2,\cdots,X_n)\in W\}=\alpha\)求解确定拒绝域\(W\).

第4步 ：由样本数据\((x_1,x_2,\cdots,x_n)\)求出统计量\(T\)的值：

• 如果\((x_1,x_2,\cdots,x_n)\in W\)，则拒绝\(H_0\)，接受\(H_1\).
• 如果\((x_1,x_2,\cdots,x_n)\in \overline{W}\)，则接受\(H_0\)，拒绝\(H_1\).

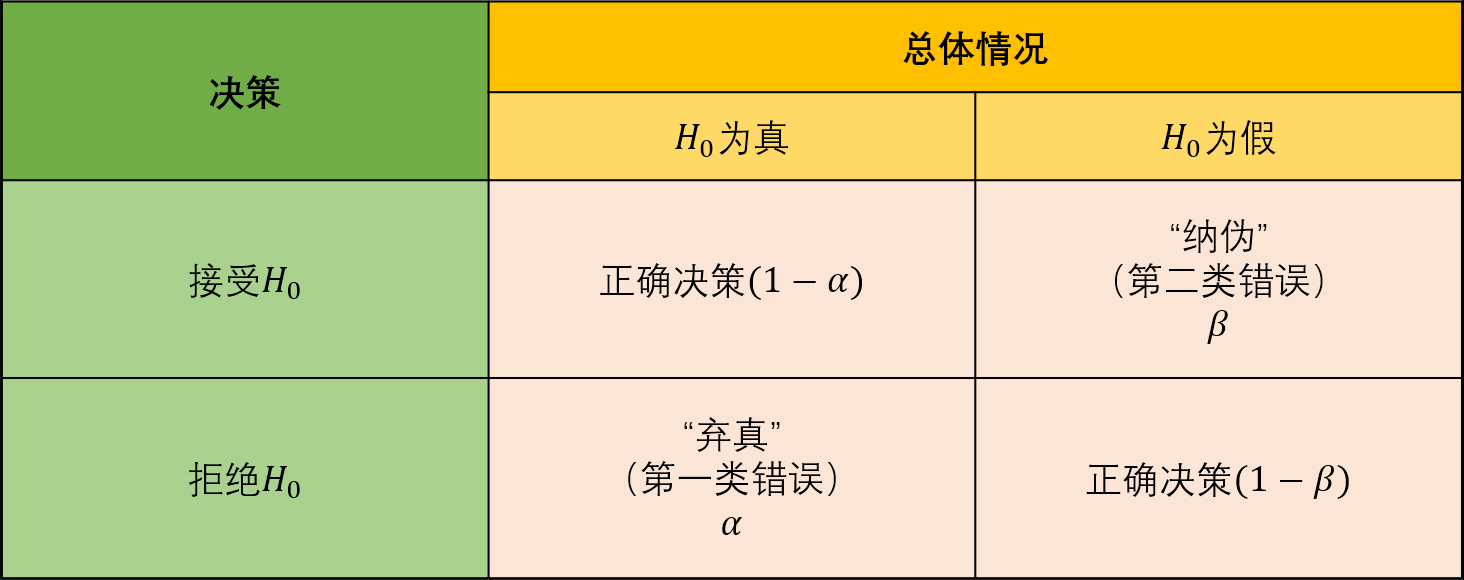
两类错误

在假设检验中，我们通过样本来检验假设的准确性。

而抽样具有随机性，并且有时样本容量过小，或者其他原因，都会导致最终的推断可能出现错误。

统计推断是具有误差的，比如天气预报。

第一类错误

弃真 ：\(H_0\)是成立的，但是被拒绝了。

犯第一类错误的概率记为：

\[P\{拒绝H_0|H_0为真\}=\alpha \]

这里的\(\alpha\)记号和上文的小概率事件的概率不是同一个记号 。

第二类错误

纳伪/取伪 ：\(H_0\)不成立，但是被接受了。

犯第二类错误的概率记为：

\[P\{接受H_0|H_0为假\}=\beta \]

目标与现实

我们希望\(\alpha\)和\(\beta\)越小越好，但是在实际问题中很难做到同时降低两个错误率，除非将样本容量\(n\)无限加大，而实际问题中抽样是需要成本的，所以很难同时降低\(\alpha\)和\(\beta\)。

通常，我们更重视\(\alpha\)，在\(\alpha\)很小的前提下，再尽量降低\(\beta\).

思路 ：宁信其有，不信其无 ，或者说严重点记作宁可杀错不可放过 。

案例 ：

1. 某刑事案件中有犯人1个，但是只要是有嫌疑的人都会被调查访问。

在这个案例中，第一类错误就是把犯人放跑了，即弃真 ；第二类错误是只要有嫌疑的人都会被调查，不管其是否真的是犯人，即纳伪 。显然我们更关注的是真的那个犯人，所以我们的首要任务是要把第一类错误的错误率压下去，即只要是有嫌疑的人都要被调查访问。

1. 体检：不确定身体有没有问题？那就检查一下。

我们不希望“生病了但是不知道自己生病了”，也就是不希望出现第一类错误。就算是没有的病，体检的时候也要检查一下，所以第二类错误在这个案例中是无关紧要的。

使用教材：
《概率论与数理统计》第四版 中国人民大学 龙永红 主编 高等教育出版社