[概率论与数理统计]笔记：5.3 置信区间

5.3 置信区间

前言

点估计无法提供其估计的误差，而区间估计可以。

案例 ：“某人的月薪比2k多，比20k少”，这就是一个区间估计。

区间估计的好坏有两个衡量指标：

• 区间长度
• 真实值落在该区间的概率

我们希望区间长度足够小，而真实值落在该区间的概率又足够大。

事实上，这两个指标是矛盾的，如果概率很大，会导致区间变大；如果区间长度变小，落在区间内的概率就会变小。

定义

\[P\{\underline{\theta}<\theta<\overline{\theta}\}=1-\alpha \]

• \(\theta\)是要估计的参数。
• \((\underline{\theta},\overline{\theta})\)是置信区间，其中\(\underline{\theta}\)是置信下限，\(\overline{\theta}\)是置信上限。
• \(1-\alpha\)是置信水平，或者叫置信度。

做题的时候一般是题目告知置信度，然后需要求解置信上下限。

表述

\((\underline\theta,\overline\theta)\)能套住 \(\theta\)的概率是\(1-\alpha\)。

这里需要区分两种表述：

1. \((\underline\theta,\overline\theta)\)能套住 \(\theta\)的概率是\(1-\alpha\)。
2. \(\theta\) 落在 \((\underline\theta,\overline\theta)\)的概率是\(1-\alpha\)。

需要明确的是，\(\theta\)虽然是未知的，但是是确定的。\(\theta\)准确地固定在数轴上的一个位置，只是我们不知道在哪里。我们使用区间\((\underline\theta,\overline\theta)\)来做多次试验，每次试验的区间是随机的不同的，因此\(\theta\)有时会被区间套住 ，有时候不会。

因此，我们使用的表述是套住 ，而不是落在 。后者是针对不确定 的值时候的表述。

---

枢轴变量

定义

为了求解置信区间，需要构造枢轴变量

\[I=I(T,\theta) \]

其中\(\theta\)是未知参数，\(T\)是已知的，\(I\) 的分布已知且与\(\theta\)无关。

对于给定的\(1-\alpha\)，确定\(F\)的上\(\frac{\alpha}{2}\)分位数，记为\(u{\frac{\alpha}{2}}\)；确定\(F\)的上\((1-\frac{\alpha}{2})\)分位数，记为\(u{1-\frac{\alpha}{2}}\)，那么就会有

\[P\{u{1-\frac{\alpha}{2}}(T,\theta)<u{\frac{\alpha}{2}}\}=1-\alpha \]

图解

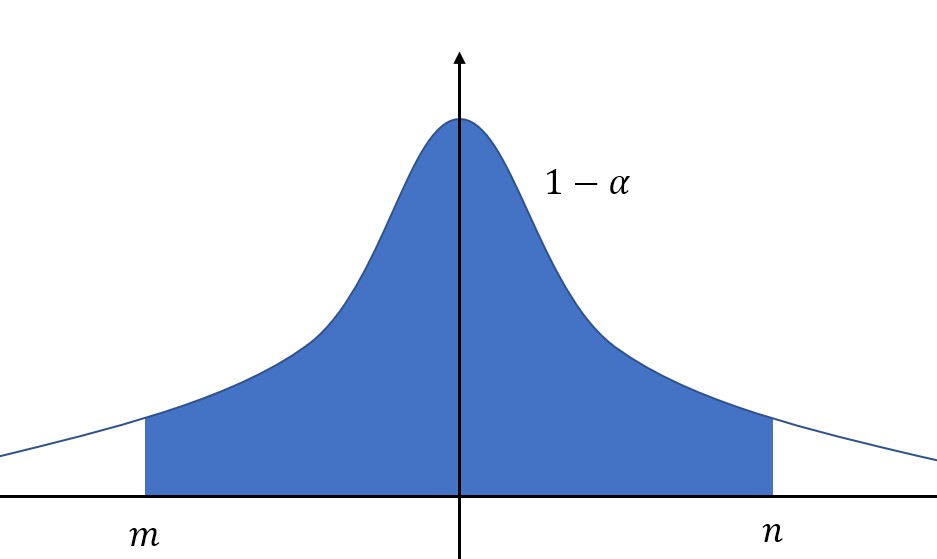
对于给定的置信度，也就是概率\(1-\alpha\)，我们的目的是求解区间上下限，也就是图中的\(m\)和\(n\)。

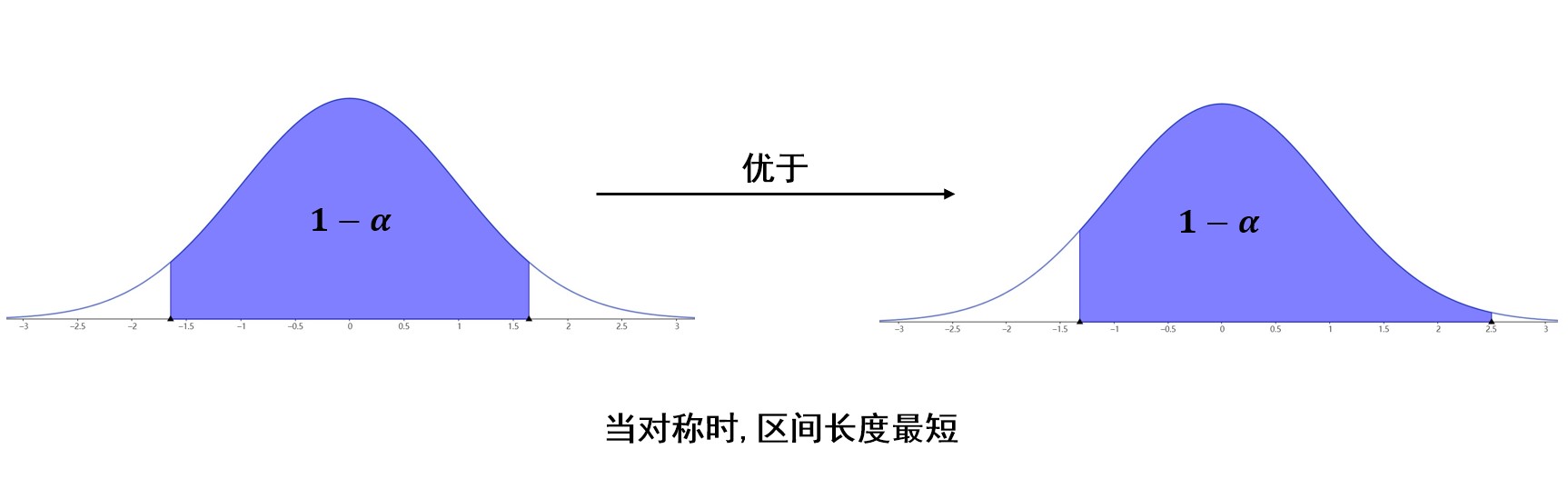
值得注意的是，我们希望区间长度小一些，如果研究的分布是正态分布，或者密度函数类似于上图，那么在置信度一定的情况下，即图中蓝色区域面积一定，只要选定区间位于中间，关于\(y\)轴对称，那么区间长度就是最小的。（因为峰值在中间）

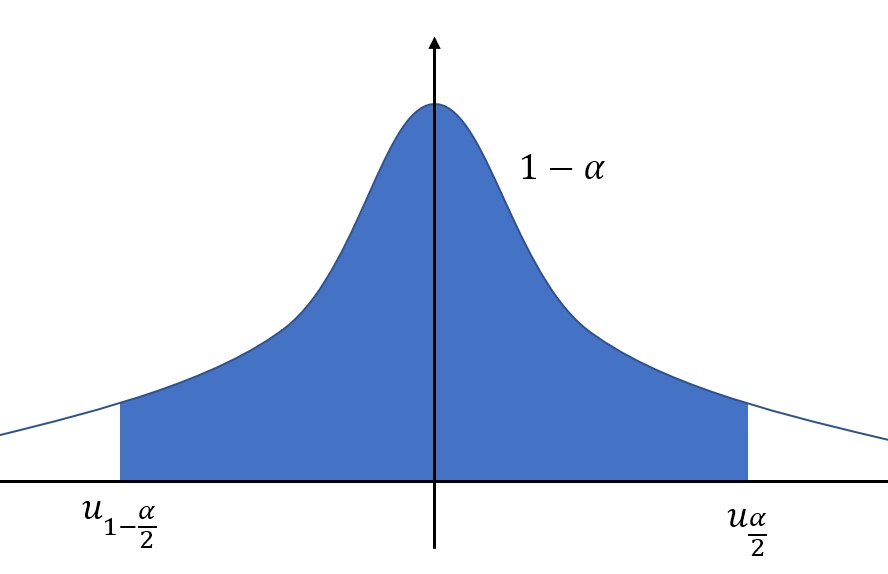
当置信区间位于中间时，置信度为\(1-\alpha\)，那么左右两个置信上下限就可以通过上侧分位数表示了。

中间的阴影面积为\(1-\alpha\)，那么左右两侧的空白面积就分别是\(\frac{\alpha}{2}\)。

置信上限使用上侧分位数表示就是：\(u_{\frac{\alpha}{2}}\).

置信下限使用上侧分位数表示就是：\(u_{1-\frac{\alpha}{2}}\).

总结

构造枢轴变量的目的是为了求解置信区间，将枢轴变量构造成我们熟悉的分布，比如正态分布，\(t\)分布，\(F\)分布。然后就可以利用这些分布的性质列出不等式，然后求解出我们要估计的参数的区间。

需要注意的是，枢轴变量只能包含一个未知的参数，即我们要估计的参数\(\theta\)，只有这样才能进行不等式化简。

---

正态总体参数的置信区间

均值\(\mu\)的置信区间

情况1：方差\(\sigma^2\)已知

总体方差\(\sigma^2\)已知，估计\(\mu\)，此时\(\mu\)是未知参数。

构造枢轴量：

\[U=\frac{\overline{X}-\mu}{\sigma/\sqrt{n}}\sim N(0,1) \]

相关知识点：👉抽样分布相关的定理的推论.

注 ：对于枢轴量\(U\)来说

• \(\overline{X}\)和\(\sqrt{n}\)由样本可以知道，是已知的。
• \(\sigma\)由于总体方差\(\sigma^2\)已知，所以也是已知的。
• \(U\)已知服从标准正态分布，该分布与未知参数\(\mu\)无关。

\(U\) 服从标准正态分布，具有对称性。

对于给定的置信度\(1-\alpha\)，可以计算得到\(\frac{\alpha}{2}\)，查表就可以得到上侧分位数\(u_{\frac{\alpha}{2}}\)的值，再根据对称性，就有

\[P\{-u{\frac{\alpha}{2}}<\frac{\overline{X}-\mu}{\sigma/\sqrt{n}}<u{\frac{\alpha}{2}} \}=1-\alpha \]

于是就可以求解出\(\mu\)的置信区间：

\[\overline{X}-\frac{\sigma u{\frac{\alpha}{2}}}{\sqrt{n}} < \mu < \overline{X}+\frac{\sigma u{\frac{\alpha}{2}}}{\sqrt{n}} \]

理解 ：

• 如果增大置信度\(1-\alpha\)，那么\(\alpha\)就会变小，于是上侧分位数\(u_{\frac{\alpha}{2}}\)会变大，代入上面的置信区间公式，就会发现置信上限变大了，置信下限变小了，即置信区间的区间长度变大了。
• 观察到样本容量\(n\)位于分母位置，于是发现样本数增加可以缩小置信区间的区间长度。但是需要注意的是实际调研中，收集样本是需要投入时间和金钱的，更多的样本意味着更高的成本。

做题思路 ：代入已知数值求解区间上下限就行了👌.

---

情况2：方差\(\sigma^2\)未知

总体方差 \(\sigma^2\)未知，那么在构造枢轴变量的时候可以转而使用样本方差 \(S^2\).

构造枢轴变量：

\[T=\frac{\overline{X}-\mu}{S/\sqrt{n}}\sim t(n-1) \]

相关知识点：👉抽样分布相关的定理

其中的\(S\)是样本标准差 。

由于\(t\)分布是具有对称性的，对于给定的置信度\(1-\alpha\)，有

\[P\{ -t{\frac{\alpha}{2}}(n-1) < \frac{\overline{X}-\mu}{S/\sqrt{n}} < t{\frac{\alpha}{2}}(n-1) \} =1-\alpha \]

同理可解得置信区间为

\[\overline{X}-\frac{S}{\sqrt{n}}t{\frac{\alpha}{2}}(n-1) < \mu < \overline{X}+\frac{S}{\sqrt{n}}t{\frac{\alpha}{2}}(n-1) \]

\(t_{\frac{\alpha}{2}}(n-1)\)是自由度为\(n-1\)的\(t\)分布的上侧\(\frac{\alpha}{2}\)分位数，可以通过查表得到。

---

方差\(\sigma^2\)的置信区间

情况1：均值\(\mu\)已知

构造枢轴变量：

\[\frac{1}{\sigma^2}\sum\limits_{i=1}^n(X_i-\mu)^2 \sim \chi^2(n) \]

相关知识点：👉抽样分布相关的定理

该枢轴变量只有总体方差\(\sigma^2\)是未知的。

注 ：卡方分布不是对称的，但是由于习惯，在选择上侧分位数的时候仍然使用选择\(\frac{\alpha}{2}\)，但是不能像正态分布或者\(t\)分布一样直接使用相反数（比如上面的\(t{\frac{\alpha}{2}}(n-1)\)和\(-t{\frac{\alpha}{2}}(n-1)\)），而是要使用\(\chi^2{1-\frac{\alpha}{2}}(n)\)和\(\chi^2{\frac{\alpha}{2}}(n)\).

\[\chi^2{1-\frac{\alpha}{2}}(n) < \frac{1}{\sigma^2}\sum\limits{i=1}^n(Xi-\mu)^2 < \chi^2{\frac{\alpha}{2}}(n) \]

可以解得：

\[\frac{\sum\limits_{i=1}^n(Xi-\mu)^2}{\chi^2{\frac{\alpha}{2}}(n)} < \sigma^2 < \frac{\sum\limits_{i=1}^n(Xi-\mu)^2}{\chi^2{1-\frac{\alpha}{2}}(n)} \]

---

情况2：均值\(\mu\)未知

总体均值 \(\mu\)未知，转而使用样本均值 \(\overline{X}\)构造枢轴变量：

\[\frac{(n-1)S^2}{\sigma^2} \sim \chi^2(n-1) \]

相关知识点：👉抽样分布 定理 2

由于样本是已知的，所以样本容量\(n\)和样本方差\(S^2\)都是已知的，只有要估计的\(\sigma^2\)是未知的。

类似地，对于给定的置信度\(1-\alpha\)，计算上侧分位数\(\chi^2{1-\frac{\alpha}{2}}(n-1)\)和\(\chi^2{\frac{\alpha}{2}}(n-1)\).

于是有

\[P\{ \chi^2{1-\frac{\alpha}{2}}(n-1) < \frac{(n-1)S^2}{\sigma^2} < \chi^2{\frac{\alpha}{2}}(n-1) \} = 1-\alpha \]

可以解得：

\[\frac{(n-1)S^2}{\chi^2{\frac{\alpha}{2}}(n-1)} < \sigma^2 < \frac{(n-1)S^2}{\chi^2{1-\frac{\alpha}{2}}(n-1)} \]

---

总结

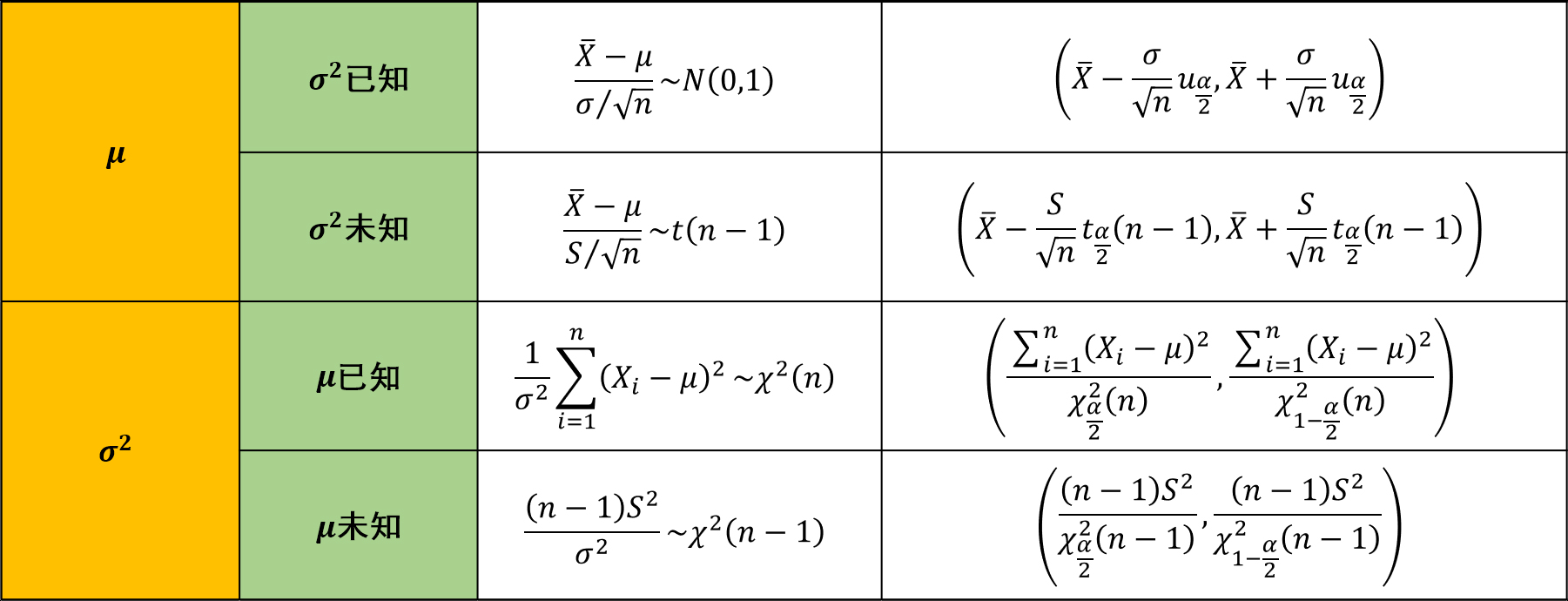
使用教材：
《概率论与数理统计》第四版 中国人民大学 龙永红 主编 高等教育出版社