[概率论与数理统计]笔记：5.5 单正态总体的参数假设检验

5.5 单正态总体的参数假设检验

均值\(\mu\)的检验

对于参数\(\mu\)可以提出如下假设：

\[\begin{align} & H_0:\mu=\mu_0 \leftrightarrow H_1:\mu\ne\mu_0 \tag{A} \
& H_0:\mu\le\mu_0 \leftrightarrow H_1:\mu>\mu_0 \tag{B} \\ & H_0:\mu\ge\mu_0 \leftrightarrow H_1:\mu<\mu_0 \tag{C} \\ \end{align} \]

其中\((A)\)的\(H_1\)，参数\(\mu\)可以取值在\(\mu_0\)两侧，称为双侧假设检验问题 。

对应地，\((B)\)和\(©\)称为单侧假设检验问题 。

情况1：方差\(\sigma^2\)已知

已知\(\sigma^2 = \sigma_0^2\)，检验\(H_0:\mu=\mu_0\).

这里先讨论双侧假设检验问题。

\[H_0:\mu=\mu_0 \leftrightarrow H_1:\mu\ne\mu_0 \tag{A} \\ \]

第1步 ：提出假设\(H_0:\mu=\mu_0 \leftrightarrow H_1:\mu\ne\mu_0\)

第2步 ：假定\(H_0\)成立，则总体\(X\sim N(\mu_0,\sigma_0^2)\)，构造统计量\(U=\frac{\overline{X}-\mu_0}{\sigma_0/\sqrt{n}}\sim N(0,1)\)

第3步 ：对于给定\(\alpha\)，由小概率事件发生概率\(P\{|U|>u\frac{\alpha}{2}\}=\alpha\)，再结合查表，可以得到\(u\frac{\alpha}{2}\)

样本均值\(\overline{X}\)是\(\mu\)的优良估计，所以二者是非常接近的。所以，\(U\)的取值应该大概率落在0附近。如果\(|U|\)超出某个阈值，我们就认为是小概率事件发生了，通过指定阈值概率\(\alpha\)，我们就可以查表得到\(u_\frac{\alpha}{2}\)，也就是确定了拒绝域。

第4步 ：计算\(U\)的值，比较\(|U|\)和\(u_\frac{\alpha}{2}\)

统计量\(U\)是通过样本计算得到的，如果计算结果\(|U|>u_{\frac{\alpha}{2}}\)，那么我们就说这个样本落在了拒绝域。

下结论 ：

• 如果\(|U|>u_\frac{\alpha}{2}\)，则拒绝\(H_0\).

• 如果\(|U|_\frac{\alpha}{2}\)，则接受\(H_0\).

• 如果\(|U|=u_\frac{\alpha}{2}\)，慎重处理，再抽样，再检验。

对于单侧假设检验问题：

\[\begin{align} & H_0:\mu\le\mu_0 \leftrightarrow H_1:\mu>\mu_0 \tag{B} \\ & H_0:\mu\ge\mu_0 \leftrightarrow H_1:\mu<\mu_0 \tag{C} \\ \end{align} \]

思路已知，步骤类似，只需稍作修改。

对于单侧假设检验问题，假定\(H_0\)成立，我们仍使用\(\mu=\mu_0\)构造统计量(零假设\(H_0\)始终包含\(\mu=\mu_0\))。

对于给定的\(\alpha\)，小概率事件有所改变：

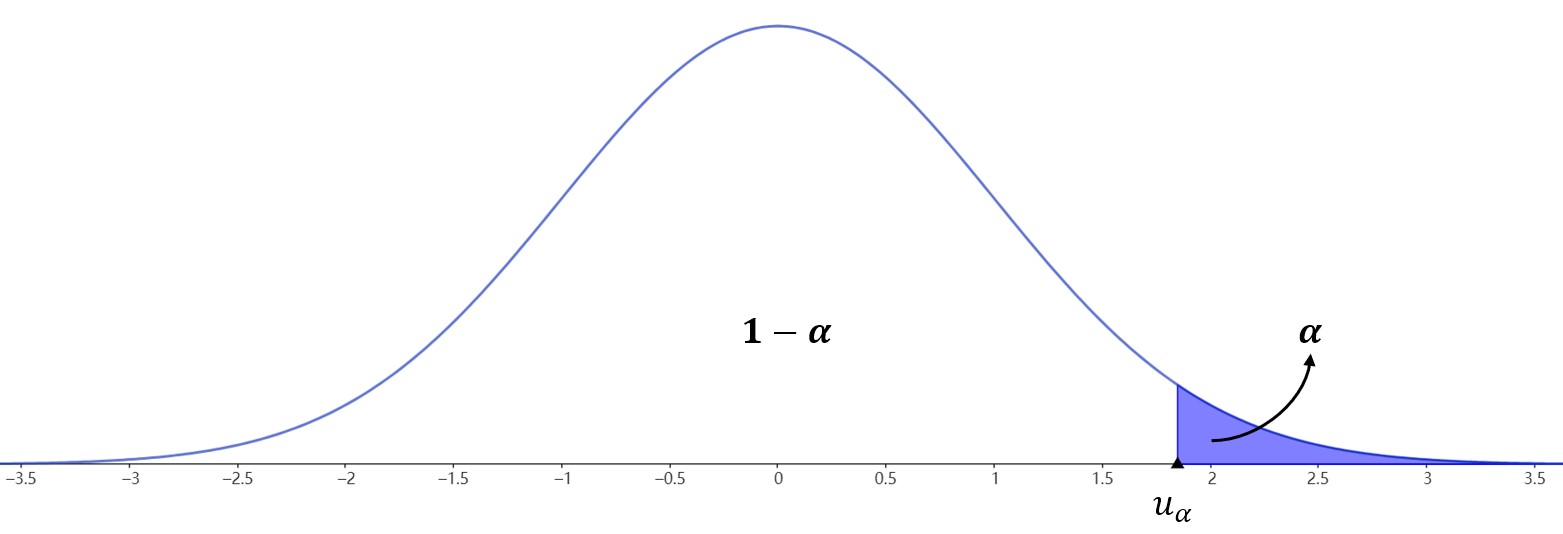
• 对于\((B)\)，\(\mu\)不能太大，所以拒绝域为\(W=\{(x_1,x_2,\cdots,xn)|U>u\alpha\}\)

• 对于\(©\)，\(\mu\)不能太小，所以拒绝域为\(W=\{(x_1,x_2,\cdots,xn)|U<-u\alpha\}\)

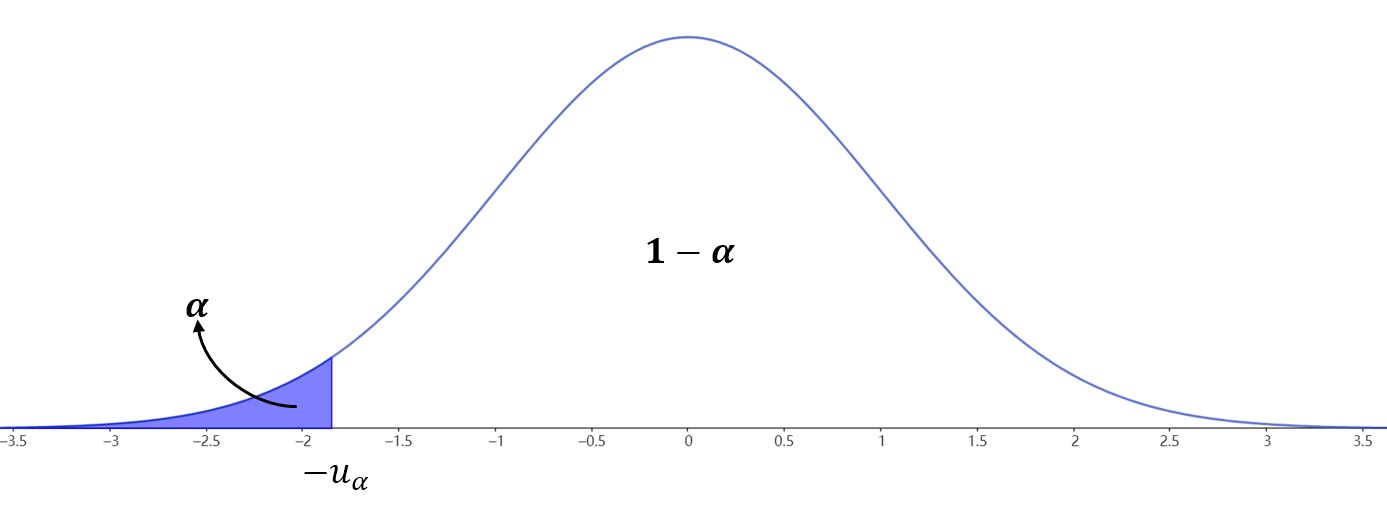
上述检验问题运用了\(U\) 检验法，即构造的枢轴量服从或者渐进服从标准正态分布 。

---

情况2：方差\(\sigma^2\)未知

总体方差\(\sigma^2\)未知，可以使用样本方差\(S^2\)来代替构造统计量：

\[T = \frac{\overline{X}-\mu_0}{S/\sqrt{n}}\sim t(n-1) \]

\(t\)分布和标准正态分布都是关于\(y\)轴对称的，所以过程与上面总体方差已知的情况类似。

不难得出\((A),(B),©\)三种情况的拒绝域：

\[\begin{align} & W=\{(x_1,x_2,\cdots,xn)|\ |T|>t{\frac{\alpha}{2}}(n-1) \} \\ & W=\{(x_1,x_2,\cdots,xn)|\ T>t\alpha(n-1) \} \\ & W=\{(x_1,x_2,\cdots,xn)|\ T<-t\alpha(n-1) \} \\ \end{align} \]

这里采用\(t\) 检验法，即构造的枢轴量服从或渐进服从\(t\) 分布。

---

方差\(\sigma^2\)的检验

对于参数\(\sigma^2\)可以提出如下假设：

\[\begin{align} & H_0:\sigma^2=\sigma^2_0 \leftrightarrow H_1:\sigma^2\ne\sigma^2_0 \tag{A} \\ & H_0:\sigma^2\le\sigma^2_0 \leftrightarrow H_1:\sigma^2>\sigma^2_0 \tag{B} \\ & H_0:\sigma^2\ge\sigma^2_0 \leftrightarrow H_1:\sigma^2<\sigma^2_0 \tag{C} \
\end{align} \]

其中\((A)\)称为双侧假设检验问题 。

对应地，\((B)\)和\(©\)称为单侧假设检验问题 。

情况1：均值\(\mu\)已知

总体均值\(\mu=\mu_0\)已知，总体\(X\sim N(\mu_0,\sigma^2)\)，检验\(H_0:\sigma^2=\sigma_0^2\).

第1步 ：提出假设\(H_0:\sigma^2=\sigma^2_0 \leftrightarrow H_1:\sigma^2\ne\sigma^2_0\)

第2步 ：假定\(H_0\)成立，则\(X\sim N(\mu_0,\sigma0^2)\)，构造统计量\(\chi^2=\frac{\sum\limits{i=1}^n(X_i-\mu_0)^2}{\sigma_0^2}\sim \chi^2(n)\)

第3步 ：对于给定的\(\alpha\)，由\(P\{\chi^2>\chi^2\frac{\alpha}{2}(n)\}=P\{\chi^2<\chi^2{1-\frac{\alpha}{2}}(n)\}=\frac{\alpha}{2}\)确定拒绝域

这里需要注意的是，卡方分布和上面的标准正态分布、\(t\)分布不同，卡方分布不是对称的。但是在双侧假设检验问题中，小概率\(\alpha\)还是被均分到了两侧，即都是\(\frac{\alpha}{2}\)，这是一个约定俗成的比例。

第4步 ：根据样本计算\(\chi^2\)值，比较拒绝域，下结论。

总结 ：

• \((A)\)的拒绝域：\(W=\{(x_1,x_2,\cdots,xn)|\chi^2<\chi^2{1-\frac{\alpha}{2}}(n)或\chi^2>\chi^2_\frac{\alpha}{2}(n)\}\)

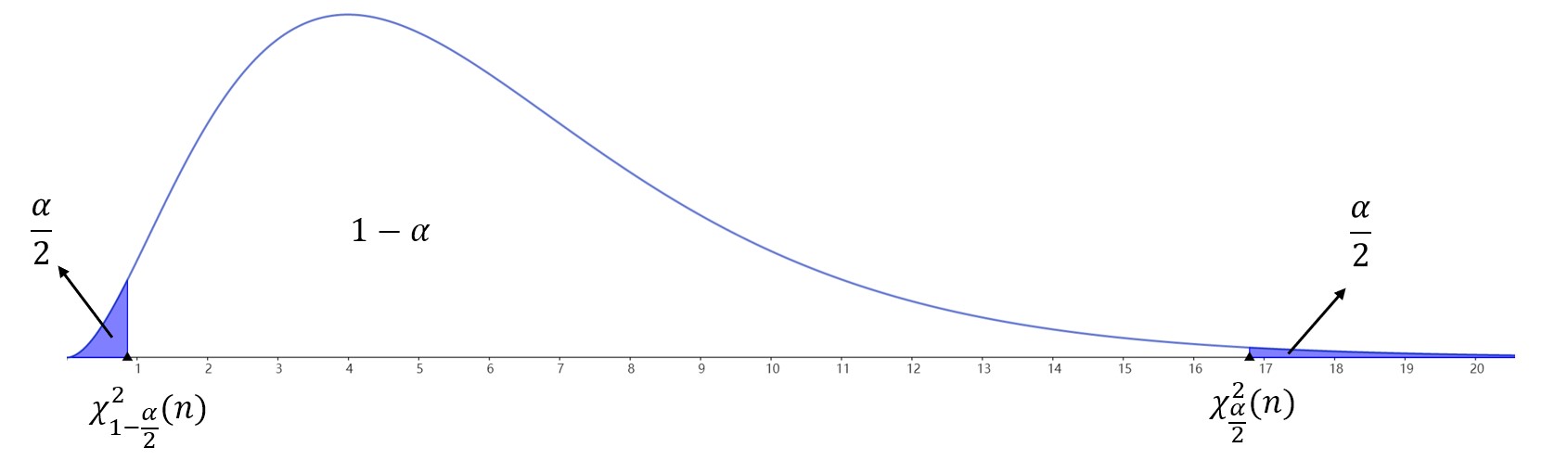
• \((B)\)的拒绝域：\(W=\{(x_1,x_2,\cdots,xn)| \chi^2>\chi^2\alpha(n)\}\)

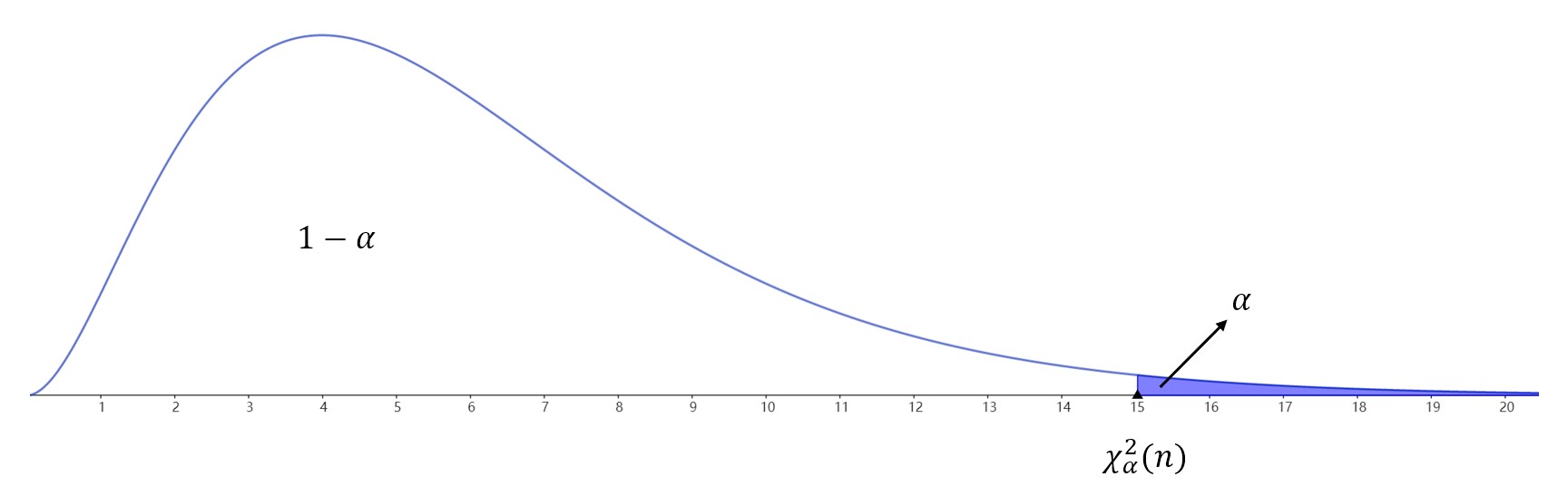
• \(©\)的拒绝域：\(W=\{(x_1,x_2,\cdots,xn)|\chi^2<\chi^2{1-\alpha}(n)\}\)

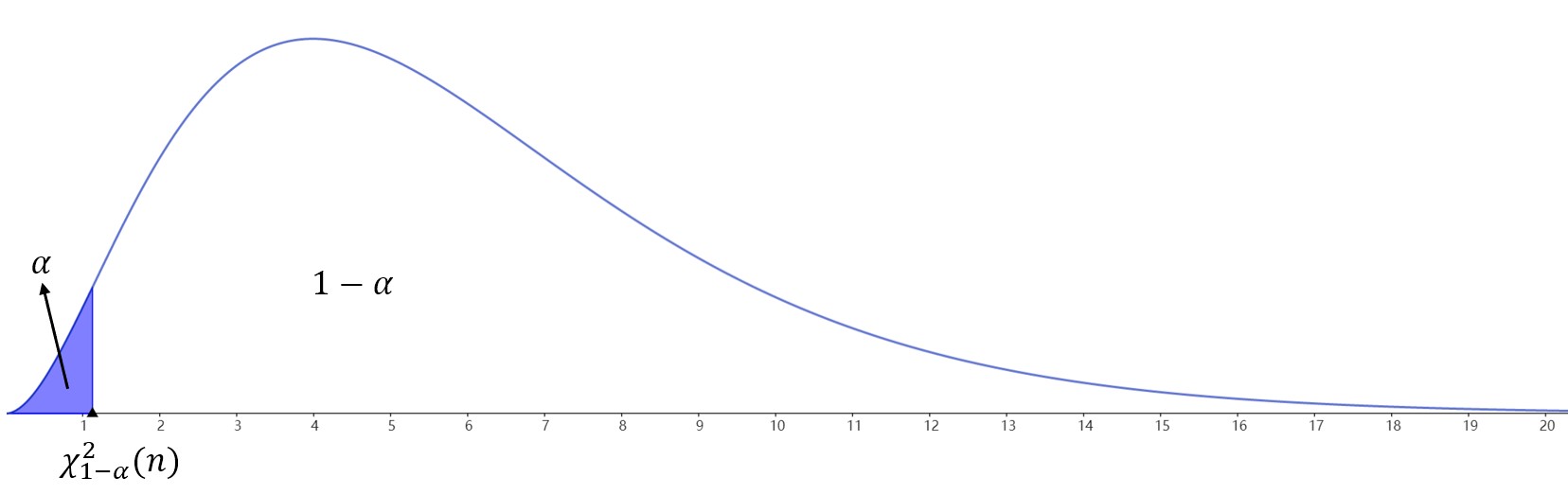
以上采用了\(\chi^2\)检验法 ，即构造的枢轴量服从或渐进服从\(\chi^2\)分布 。

---

情况2：均值\(\mu\)未知

由于总体均值未知，构造统计量的时候可以用样本均值\(\overline{X}\)代替。

假定\(H_0:\sigma^2=\sigma_0^2\)成立，构造统计量：

\[\chi^2 = \frac{\sum\limits_{i=1}^n(X_i-\overline{X})^2}{\sigma_0^2}\sim \chi^2(n-1) \]

过程与上文类似，可以得出\((A),(B),©\)三种情况的拒绝域分别是：

\[\begin{align} & W=\{(x_1,x_2,\cdots,xn)|\chi^2<\chi^2{1-\frac{\alpha}{2}}(n-1)或\chi^2>\chi^2_\frac{\alpha}{2}(n-1)\} \\ & W=\{(x_1,x_2,\cdots,xn)| \chi^2>\chi^2\alpha(n-1)\} \\ & W=\{(x_1,x_2,\cdots,xn)|\chi^2<\chi^2{1-\alpha}(n-1)\} \\ \end{align} \]

这种情况下也是采用了\(\chi^2\)检验法，与总体均值\(\mu\)已知的情况只区别于自由度分别为\(n\)和\(n-1\).

使用教材：
《概率论与数理统计》第四版 中国人民大学 龙永红 主编 高等教育出版社