目录

• 逐像素遍历光源 or 绘制光源形状
  • 逐像素遍历光源
  • Draw Light Volume（绘制光源形状）
• Tile-based Light Culling
  • Culling 流程
    • Injection Pass [逐 tile 收集]
    • Injection Pass [逐光源注入] [可选]
    • Compact Pass
  • 2.5D Culling
  • Fine Pruned Tiled Light Lists（FPTL）
• Cluster-based Light Culling
  • Culling 流程
    • Cluster Visibility [可选]
    • Injection Pass
    • Compact Pass
• Draw Light Volume
  • Double-Pass Stencil Culling
  • Depth Bounds Test
  • Instancing
• 相交检测优化
  • Sphere-Frustum Test
  • Cone Test
  • Spherical-sliced Cone Test
• UnrealEngine 5.1 多光源源码剖析
  • Cluster-based Light Culling
  • Draw Light Volume
• 更多 idea
  • 相交检测优化
  • Light Culling 相关结构的优化
  • Light Culling in GI
  • Normal-based Light Culling
• 参考

逐像素遍历光源 or 绘制光源形状

在计算延迟渲染管线的直接光照时，一般有两大类策略。本节之后将进一步剖析两类方法的改进。

逐像素遍历光源

往往基于 compute shader。需要逐 pixel 遍历所有光源并将每个光源的贡献加起来作为本 pixel 的直接光照值。

1 shading pass:
for each pixel in screen
    read G-buffer
    for each affecting light
        compute shading
    write frame buffer

当场景含有大量光源时，这种粗暴的遍历所有光源会导致巨大的性能开销。这时候就需要搭配 light culling 方法来剔除掉大量不会造成贡献的无关光源。

缺陷：

[×] 建立 light culling 结构本身也需要一定开销（例如逐 tile 遍历光源列表等）。因此场景只有少量几个光源时，最好采用绘制光源形状策略；而光源数量较多时，使用 light culling 方法带来的收益才能大于建立结构的开销。

[×] light culling 需要硬件支持 CS 中的一些特性，在一些旧移动端机器上跑不了。

Draw Light Volume（绘制光源形状）

基于 graphics pipeline。Draw Light Volume 的原理是，为每个光源影响范围建成 mesh，并绘制它们。往往是 1 个光源 1 次 draw call，并在 pixel shader 中计算本光源对该 pixel 的光照贡献，并以加法混合的形式叠加到 frame buffer 上。

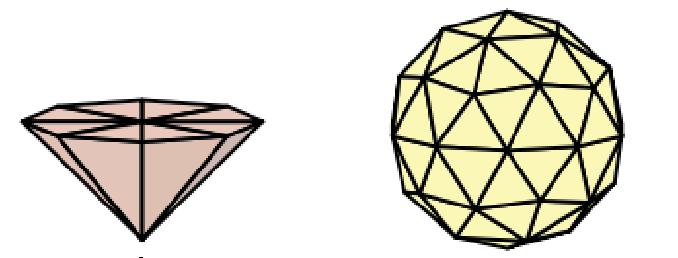
如下图左为 spot light 的光源形状，下图右为 point light 的光源形状，它们都可以根据光源影响范围、张角等来调整对应光源形状模型的变换。

n lighting pass(n Draw Calls):
for each fragment
    read n/m-buffer
		compute shading
    write accumulated buffer

虽然这种方式看起来会让像素避开无关光源的计算，但也可能会有以下缺点：

[×] 过多的 draw call： n 个光源至少要 n 次 draw call，甚至有些方法是需要 2n 次。

[×] 另一种带宽开销：假设 n 个光源覆盖在同 1 个 pixel，那么计算该 pixel 的光照就需要读 n 次 G-Buffer，而在逐像素遍历光源策略中只需要读 1 次。

Tile-based Light Culling

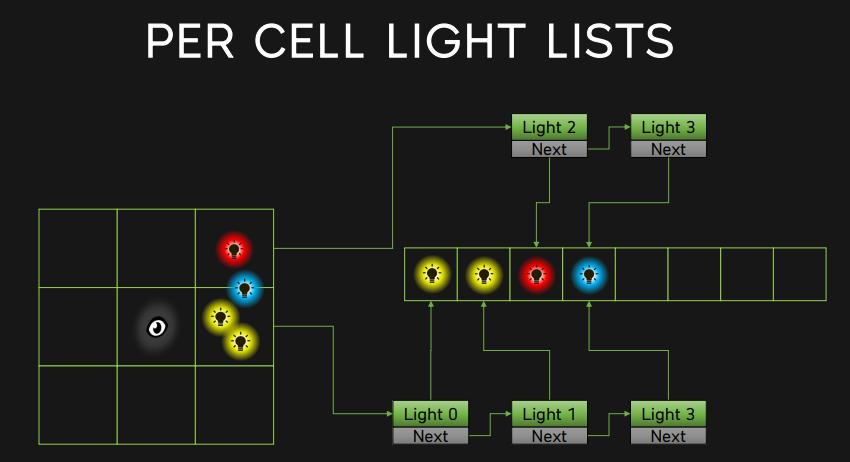
Tiled-based Light Culling 将屏幕区分划分为多个 tile ，且每个 tile 拥有⼀个光源列表（包含所有在该 tile 内有影响的光源）。

这样就可以在对某个 fragment 着色时，算出该 fragment 所在的 tile，就能找到 tile 对应的光源列表，并对列表里的光源进行光照贡献计算，而不必对整个场景的所有光源进行光照贡献计算。

每个 tile 覆盖的区域为 32×32 pixels ，也可以是别的分辨率。

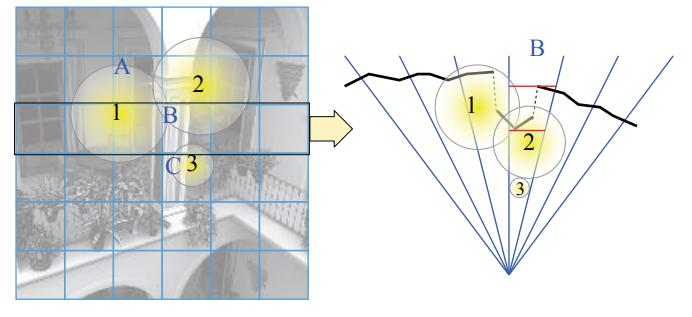
不过，当摄像机（或者光源）位置和方向发生改变，所有 tile 都需要重新计算其光源列表。

Tiled-based Light Culling 优缺点 ：

[√] 减少了相当部分的无关光源的计算。

[×] 基于屏幕空间的 tile 划分仍然粗糙，没有考虑到深度值（离摄像机远近的距离）划分。

如下图黑色线段物体，每个 shading point 本应该最多同时受到一个光源的影响，由于 tile 划分没有考虑 z 值，从而使得实际每个 shading point 都有三个光源的着色计算：

Tiled-based Light Culling 数据结构 ：

• GlobalLightList ：存储着各光源的属性（如 radiant intensty 等）
• TileLightIndexBuffer ：存储着各 tile 对应的光源 ID 列表，以数组的形式拼接在一起
• TileBuffer ：某个 tile 的光源 ID 列表位于 tile 光源索引列表的哪里到哪里（数组中下标多少到多少）

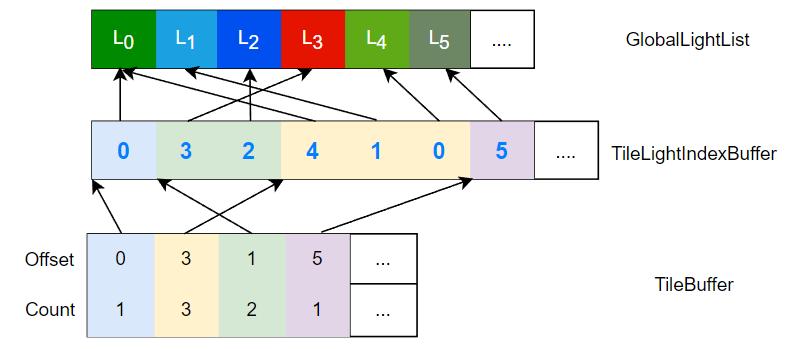
我们要做的，便是想办法建立并填充这个数据结构，以便在后续的着色流程使用（例如可以在 pixel shader 中判断自己在哪个 tile 然后访问 tile 对应的光源列表来 cull 掉大量光源）。

Culling 流程

一种最常见的实现方式便是基于 linked list，通常包含 injection pass 和 compact pass。

Injection Pass [逐 tile 收集]

Injection Pass [compute shader]：

• 1 thread <=> 1 pixel
• 1 thread group <=> 1 tile

为了方便说明，假设 8x8 threads 为 1 group，即 1 个 tile 含 8x8 pixels。

1. 每个 pixel 拿自己的深度对 group shared 的 zmin, zmax 做原子min, max操作，group sync 后的 zmin, zmax 便代表了这个 tile 的最大和最小深度值。
2. 根据 tile 最大最小深度值，构造这一 tile 的视锥体。
3. 由于 1 个 tile 需要对 N 个光源做相交检测，而 tile 具有 8x8 threads，为此应当让每个 thread 处理 \(\lceil \frac{N}{8×8} \rceil\) 个光源的相交检测。当 thread 在检测某一光源对tile有影响时，将通过测试的光源索引 LightIndex 添加进 tile 对应的 Tile Linked List。

而在 compute shader 实现 Linked List，需要一些技巧：

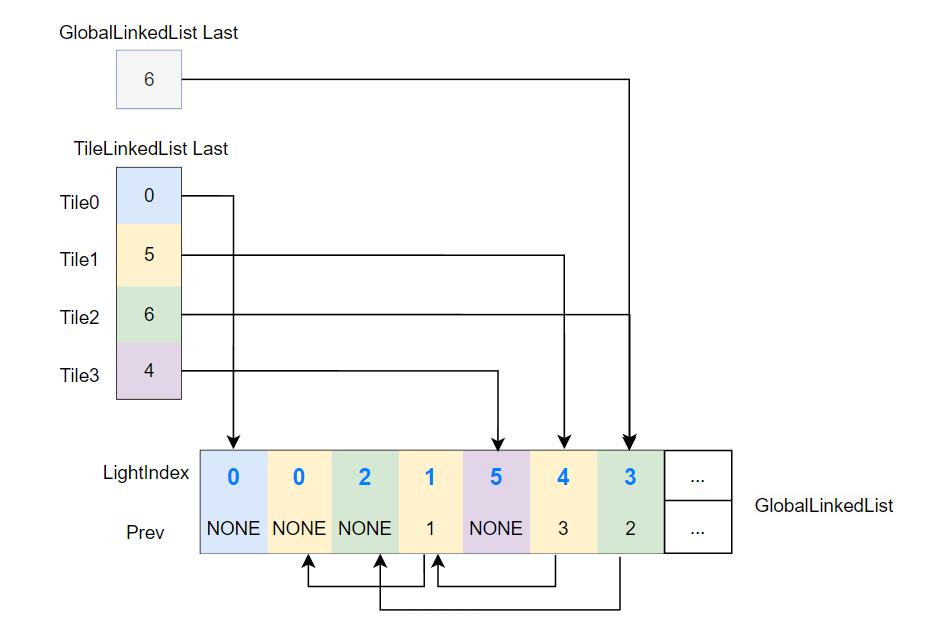
• 使用 Global Linked List（实际上是一个预分配好的 buffer）来实际存储所有 links，并通过 GlobalLinkedListLast 来指向 buffer 里最后一个 link。
• TileLinkedListLast 指向对应 tile 的 linked list 的最后一个 link，link 的 prev 属性只会指向同一 tile 的前一个 link，这样就可以保证各个 tile 对应的 tile linked list 各自独立。

GlobalLinkedListLast 和 TileLinkedListLast 这种需要跨线程乃至跨线程组来共享的全局变量，一般用 RWByteAddressBuffer 来存储，这样 compute shader 的各个线程都能访问这个 RWByteAddressBuffer ，从而来对这个共享的全局变量进行读写。

也就是说将 LightIndex 添加进 Tile Linked List 实际上在做的是：

// 从 Global Linked List 分配一个 link 的空间
nextLink = 0
InterlockedAdd(GlobalLinkedListLast, 1, nextLink)
// 拿到 Tile Linked List 的最后一个 link
previousLink = 0
InterlockedExchange(TileLinkedListLast[tile.pos], nextLink, previousLink)
// 写入 link
GlobalLinkedList[nextLink].lightIndex = light.Index
GlobalLinkedList[nextLink].prevLink   = previousLink

Injection Pass [逐光源注入] [可选]

逐 tile 收集的 injection pass 在遇到海量光源（光源数量远远大于tile数量）时可能有性能问题，因为需要每个 thread 需要遍历太多光源了，指令过长，对 GPU 计算非常不友好。因此这里提供第二种 injection pass 的实现方式，其核心思想就是将 tile 收集 lights 的关系转换成 light 注入 tiles 的关系，减少单个线程的遍历次数。

不过光源数量远远大于 tile 数量的场景情况实在太少，因此本方法也只是一个思路参考。

Injection Pass [compute shader]：

• 1 thread group <=> 1 light

假设 8x8 threads 为 1 group。

1. 每个光源需要计算它可以影响到的 tiles，为此应当让每个 thread 处理 \(\lceil \frac{NumTile}{8×8} \rceil\) 个 tiles 的相交检测，将当前光源的 LightIndex 添加进通过测试的 tile 对应的 Tile Linked List。

Compact Pass

经过 injection pass 后，虽然有了同样记录 light index 的 linked list 数据结构，但是在后续的 shading 流程中，要是直接遍历这些 linked list 会带来以下缺点：

• 占用空间多：一半的空间用于存放 prev
• 极度 cache 不友好：linked list 跳跃式的遍历 link 导致 cache 命中极低

因此，我们最好增加一个 compact pass 用于 compact（紧凑）一下 linked list 成章节开头的 TileLightIndexBuffer 和 TileBuffer 数据结构。

Compact Pass [compute shader]：

• 1 thread <=> 1 tile

1. 遍历 Tile Linked List，统计该 tile 的光源数量。

   tileLightCount = 0 foreach link in TileLinkedList tileLightCount++

而遍历 tile 对应的 Tile Linked List 的伪代码如下：

link = TileLinkedListLast[tile.pos]
while link != NONE
  do something with link
  link = GlobalLinkedList[link].prevLink

1. 对 GlobalTileLightIndexCount 进行加法原子操作来实现占位，并记录 tile 在 TileLightIndexBuffer 的 offset。

GlobalTileLightIndexCount 也是跨线程共享的全局变量。

// 占位
tileLightOffset = 0;
InterlockedAdd(GlobalTileLightIndexCount, tileLightCount, tileLightOffset)
// 记录 count 和 offset
TileBuffer[tile.pos].count = tileLightCount
TileBuffer[tile.pos].offset = tileLightOffset

1. 再次遍历 Tile Linked List，在占好的位写入通过测试的光源 ID 就完事了。

   nodeCount = 0 foreach node in TileLinkedList TileLightIndexBuffer[tileLightOffset + tileLightCount - nodeCount - 1] = node.lightIndex nodeCount++

2.5D Culling

传统的 tile 包围盒只是简单通过 tile 的 min/max depth 来确定包围盒，这会导致包围盒包含了很多空腔区（即实际上没有表面 pixel 的地方），这样光源仅影响到空腔区的情况下，仍然会判定与该 tile 相交。

2.5D culling ≠ cluster-based culling，因为 2.5D 仍然是基于 tile 为单位的，只是剔除了一部分空腔区。

一个改进的做法就是，在 depth 上进行区域划分，然后根据 tile 内每个像素的 depth 来确定覆盖了哪些区域，并通过 depth mask 来编码。

在做光源与 tile 的相交检测时，光源也同样可以根据光源范围来编码成 depth mask，然后将测试的结果即为 \((\mathrm{depthmask{tile}}\ &\ \mathrm{depthmask{light}})!=0\)

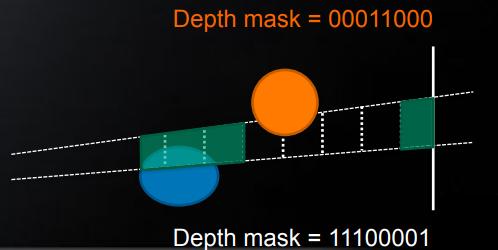
2.5D culling 效果图：

这种 tile-based culling 的改进思路虽然看着很直觉也很简单，然而带来的 culling 效率提升却是不小的，尤其是对于植被的渲染（往往空腔区特别多）。

Fine Pruned Tiled Light Lists（FPTL）

传统 tile-based light culling 将根据 tile 的最近最远深度来构造一块锥体（以 tile 为粒度）并用于建立 culling 结构，而 FPTL 旨在建立更精确的 light culling 结构，达到以 pixel 为粒度的精确剔除。

FPTL pass 的核心流程主要是：

1. 逐 tile 遍历光源列表时，只读取对应光源的 screen space AABB 信息来进行 coarse culling（粗略剔除），并将通过测试的 LightIndex 添加到 group shared 的 coarse list。

每个光源的 screen space AABB 信息可以在 CPU 提前算好也可以在 GPU 用额外一个 pass 算。原文是在 GPU 里算。

1. tile 内逐 pixel 遍历 tile 的 coarse list 时，读取对应光源的完整信息（如 spot light 的最远距离，张角等），来做更精细的剔除测试（pixel 与真正的光源形状的相交）。并将测试结果以 bit 的形式进行原子位或运算到 group shared 的 bitmap 上。

2. 最后 tile 根据 bitmap 结果，输出对应的 light indexes 便为该 tile 的光源列表。

个人认为第 2 步比较浪费，光源从AABB精细化到真正形状是可以理解的，但没必要做 tile 到 pixel 级别的精细化，因为后续 shading 也是 pixel 级别的，何不如在后面的 shading 阶段再做精细化相交检测。

当然 FPTL 也有可取的思路：

• 减少带宽读：先读取内存尺寸较小的光源AABB信息做粗剔除，过了一遍粗剔除后对所剩无几的光源才读取内存尺寸较大的光源完整信息来进行细剔除。

Cluster-based Light Culling

为了进⼀步剔除光源数量，cluster-based 在 tile-based 的基础上，将像素分组的划分从 2D 的屏幕空间扩展到 3D 的观察空间。

每个 3D 的块称为⼀个 cluster，从而使每个光源真正做到仅影响其局部区域：

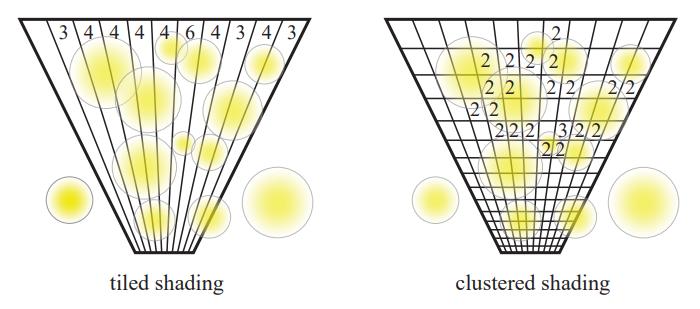
由于摄像机的透视投影，对于同样大小的物体，较远物体在屏幕上所占的空间更小；因此每个 cluster 不应该是均匀划分的，而是在深度方向上以指数形式划分（即更远处的 cluster 体积更大）

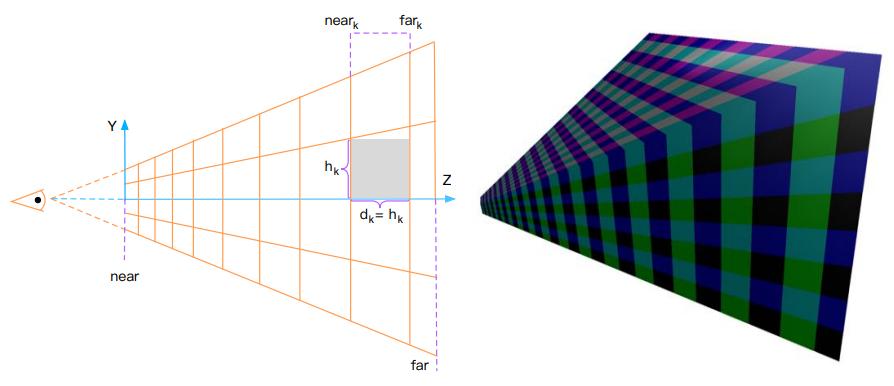
为了索引到一个 cluster，就必须有一个三维坐标来表示 \((i,j,k)\) ；\(i,j\) 其实和 tile-based 的索引映射没有区别，而需要解决的问题是：给定一个深度值 \(z\)，其在深度方向的索引值（即 \(k\) ）该如何计算？

结论：

\[k=\left\lfloor\frac{\log \left(-z\ / \text { near }\right)}{\log \left(1+\frac{2 \tan \theta}{S_{y}}\right)}\right\rfloor \]

其中，near 是近平面的深度，视锥体的 \(Y\) 方向上的张角为 \(2\theta\)， \(S_y\) 为屏幕空间 \(Y\) 方向划分的数量

以下是推导过程：

\(near_k\) 为 \(Z\) 方向上第 \(k\) 层 cluster 的近平面在 \(Z\) 方向上的值：

\[near{k}= near{k-1}+h_{k-1} \]

\(h_k\) 为在 \(Z\) 方向上第 \(k\) 层其中一个 cluster 的近平面长度。

其中第 0 层 cluster（即朝摄像机的那面位于近平面的 cluster）有：

\[near_0 = near \]

\[h{0}=\frac{2 \text { near } \tan \theta}{S{y}} \]

\[hk = \frac{h{k-1}*2*tan\theta}{Sy}+d{k-1} \]

又

\[d{k-1}=h{k-1} \]

则

\[\operatorname{near}{k}=\operatorname{near}\left(1+\frac{2 \tan \theta}{S{y}}\right)^{k} \]

此时，索引值 \(k\) 可被解出来：

\[k=\left\lfloor\frac{\log \left(-z\ / \text { near }\right)}{\log \left(1+\frac{2 \tan \theta}{S_{y}}\right)}\right\rfloor \]

Cluster-based Light Culling 优缺点：

[√] culling 效率更高：进一步剔除了更多无关光源（相比 tile-based 多考虑了深度的划分）

[x] culling 流程更加耗性能和占用显存更大：clusters 的数量远远多过 tiles，而每个 cluster 都要做光源相交检测，带来的性能开销大大增加。

Cluster-based Light Culling 数据结构 ：

基本和 tile-based light culling 的数据结构大同小异，只不过 clusters 的数量比 tiles 要多得多，buffer 的 size 也自然大得多。

Culling 流程

总体上 cluster-based culling 流程和 tile-based culling 流程差不多，只不过由于 clusters 数量远比 tiles 数量要多得多，性能开销较大（每个 cluster 都要和所有光源进行相交检测），我们可以选择增加 Cluster Visibility Pass 来剔除掉部分无关的 clusters。

当然，不走 visibility，直接对所有 cluster 进行相交检测也是可以的；是否增加该 pass 的核心在于这个 cluster visibility pass 带来的收益是否能抵消掉其带来的额外开销，而这往往需要实机测试。

Cluster Visibility [可选]

Cluster Visibility Pass [compute shader]：

• 1 thread <=> 1 pixel

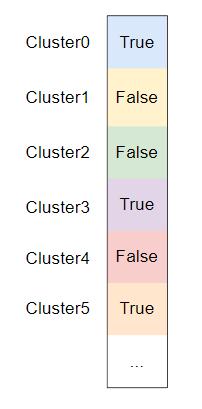
首先，我们需要找出所有参与计算的 cluster ，因为屏幕上的所有像素所涉及到的 clusters 数量一般远远小于空间中所有 cluster 的总数量（换句话说实际上能用上场的 clusters 是少部分的），我们只需要对会参与 shading 计算的 clusters 进行光源分配。

每个屏幕 pixel 计算出 cluster index 将索引到对应的 cluster 并标记为 visible：

Cluster Visibility Compact Pass [compute shader]：

• 1 thread <=> 1 cluster

有了上述记录 cluster visibility 的数组后，就可以 compact 成一个只记录 visible cluster index 的数组，方便后续的流程进行 indirect dispatch。

这里还可以使用 LDS（local data share）优化。

Injection Pass

Injection Pass [compute shader]：

1 thread <=> 1 visible cluster

基本与 tile-based 类似（遍历光源，相交测试通过后添加进 linked list）。

Compact Pass

Compact Pass [compute shader]：

1 thread <=> 1 visible cluster

与 tile-based 类似（把 linked list compact 成 cluster light index buffer 和 cluster buffer）。

Draw Light Volume

naive 的 draw light volume 可能会在 pixel shader 中进行相交检测（检测 pixel 是否在当前 volume 影响范围内），通过了则执行光照计算并将结果 add blend 到 frame buffer 上，不通过检测则 discard 掉。然而这种分支行为会让该 shader 的并行性较差，导致很多 warp stall。为此，业界常利用硬件深度测试（和模板测试）来进行相交检测，一能避免编写相交检测代码，二能大大减少 warp stall 现象。

Double-Pass Stencil Culling

我们需要真正着色的像素，其实是深度值大于 light volume 背面，小于 light volume 正面的那些 pixels。最常见的做法莫过于 double-pass，同时它也是剔除无关 pixels 的最精确方案，但缺点是每个光源要两次 draw call。

这里发现深度方向写错了，为了统一说辞，这里假设使用了 reversed-z 的技术（即深度1为近平面，深度0为远平面）。

星穹铁道也是采用这种方式，见 【星铁】截帧浅析 - 知乎 (zhihu.com)。

• Stencil Pass。对深度大于正面的 pixels 进行标记（用写入模板的形式），以便于下一个 pass 利用这个中间结果。

  • 绘制 light volume 的正面。

  • 深度测试状态：比较操作为 GREATER_EQUAL，但不写入深度。

  • 模板测试状态：比较操作为 ALWAYS （无需比较，永远通过测试），并在模板和深度测试均通过的情况下写入模板值。

  • pixel shader：不用做任何操作（因为深度测试和模板测试就是这个pass的全部操作）。

在具体实现时还要注意 light volume 刚好包围了 camera 的 case，这时候 double-pass 的方式是错误的（因为在 stencil pass 中会错误的剔除掉一些 pixels） 。因此，该 light 应该只用单面检测的 shading pass，而不应该包含 stencil pass。

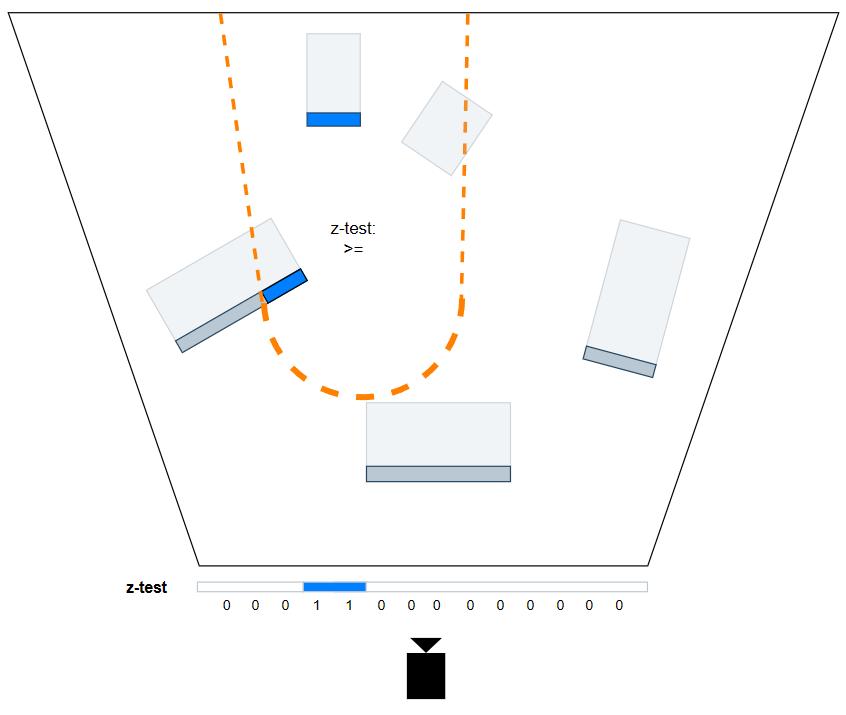
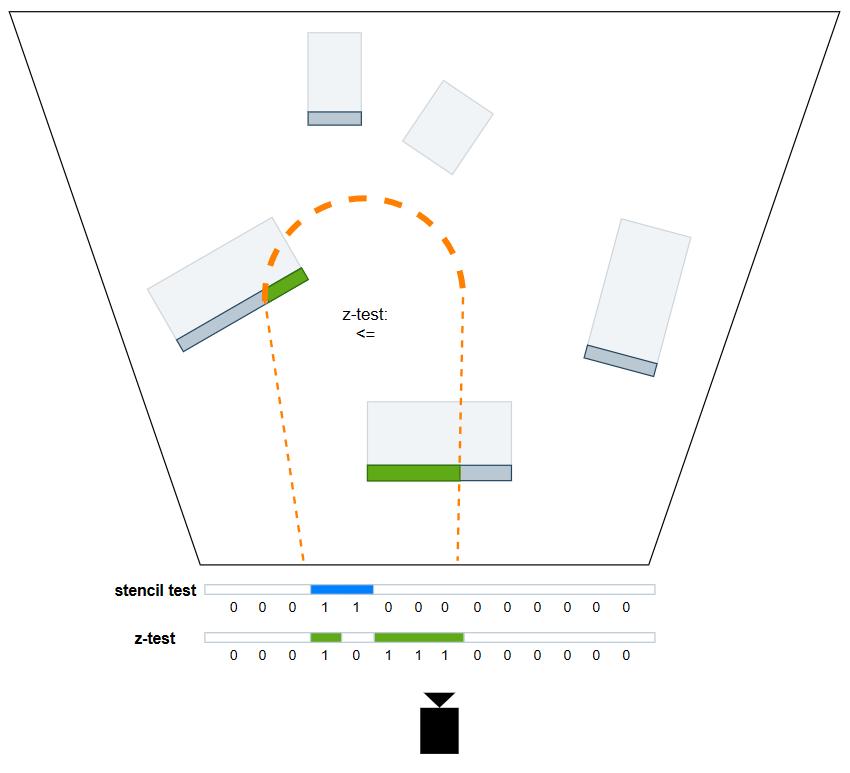
• Shading Pass。利用上一个 pass 输出的中间结果，再加一次深度小于背面的测试，就可以达成只有深度值小于 light volume 背面，大于 light volume 正面的 pixels 才会调用 pixel shader 来进行 shading。这样一来，就能够精确标记并减少light shader的浪费。
  • 绘制 light volume 的背面。
  • 深度测试状态：比较操作为 LESS_EQUAL，同样不写入深度。
  • 模板测试状态：比较操作为 EQUAL ，但不写入模板值。
  • pixel shader：光照计算，add blend

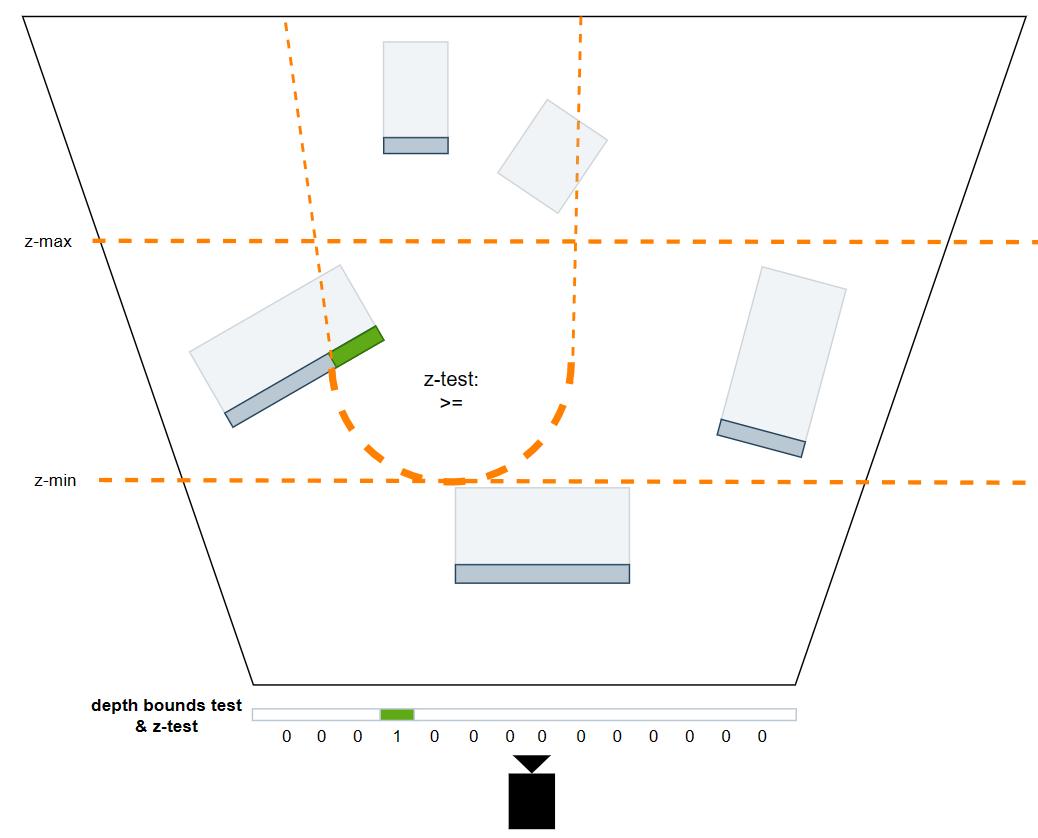
Depth Bounds Test

硬件特性 depth bounds test ：在 z-test 的基础上额外增加一种测试，将用 fragment depth 和 depth bound test 设置的 zmin 和 zmax 值作比较，如果 depth 值没有落在 [zmin, zmax] 这个区间内，则直接测试不通过。

但博主并不确定 depth bounds test 有哪些硬件设备能够支持，但至少直到 PC 显卡一般是支持的。

利用这个硬件特性，我们可以在 draw 每个光源的时候，在 CPU 计算它的 depth bound 并设置给 graphics pipeline。再搭配上 GREATER_EQUAL 的深度测试，就能有如下图的区间交集，虽然剔除精确度不如 double-pass stencil culling，但是很多时候也足够了，并且该方案可以让每个光源只用一次 draw call。

Instancing

无论是 double-pass stencil culling 还是利用 depth bounds test，draw light volume 的 draw call 次数往往都比较高（复杂度为 n 个光源），而一个改进的思考在于利用 instancing 来减少 draw call 次数。

然而，naive 的 draw light volume instancing 往往性能开销更大：

• 假如在 pixel shader 中进行相交检测并由此决定是否 discard，还是会有本节开头所说的 warp stall 问题。

• 假如结合 double-pass 方法，那么在 instancing 的 stencil pass 之后，会得到多个光源合并的 stencil buffer，从而导致后续某个光源 shading 时会产生 overdraw：

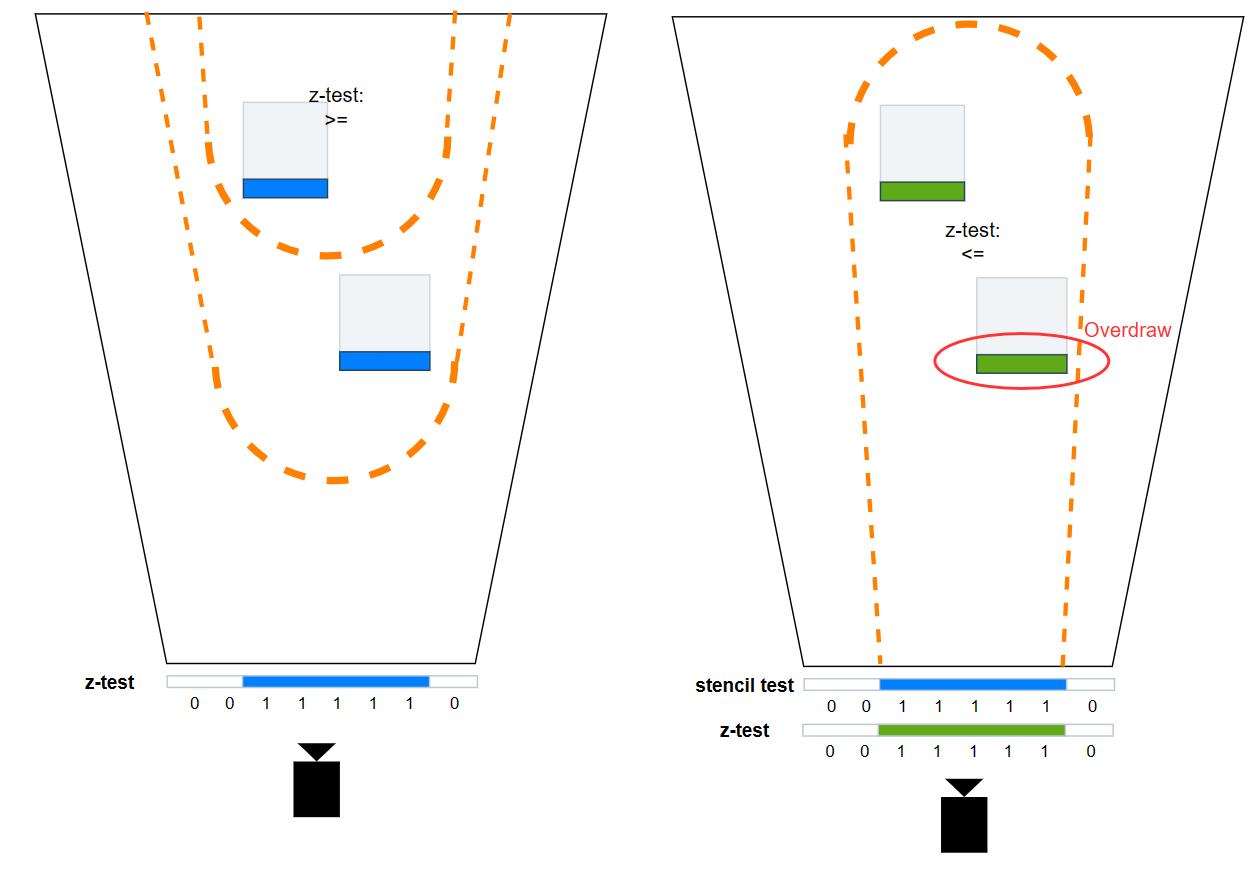
• 假如结合 depth bounds test 方法，就得将 zmin, zmax 分别设置为所有光源中的最近深度和最远深度，而这个 depth bounds 范围对某单个光源来说往往是偏大的，也会产生 overdraw。

究其原因是因为多个光源一旦处在前后遮挡关系，导致信息重叠在同一 pixel，从而容易出现 overdraw。

因此，我们要做的就是尽量避免光源信息重叠，可以考虑使用分层的思路：在 CPU 就预先对所有光源进行深度方向上的分层（根据光源的最近深度，分为 m 层），然后一层层进行 instancing 处理。这样在同一层内，光源之间会更少出现前后遮挡关系。

具体怎么对每层的光源进 instancing 处理，例如可以结合 double-pass 方法：

1. 对该层次所有光源进行 instancing 的 stencil pass，在进行 instancing 的 shading pass。
2. 该层处理完则转到更高层处理（如果该层没有光源则甚至没有 draw call 可以直接跳过）。

从最远处层级处理到最近层级的过程中，甚至是可以不需要重置 stencil buffer 的；但从最近处处理到最远处则需要每层处理重置 stencil buffer。这个为什么可以自己去想 😃

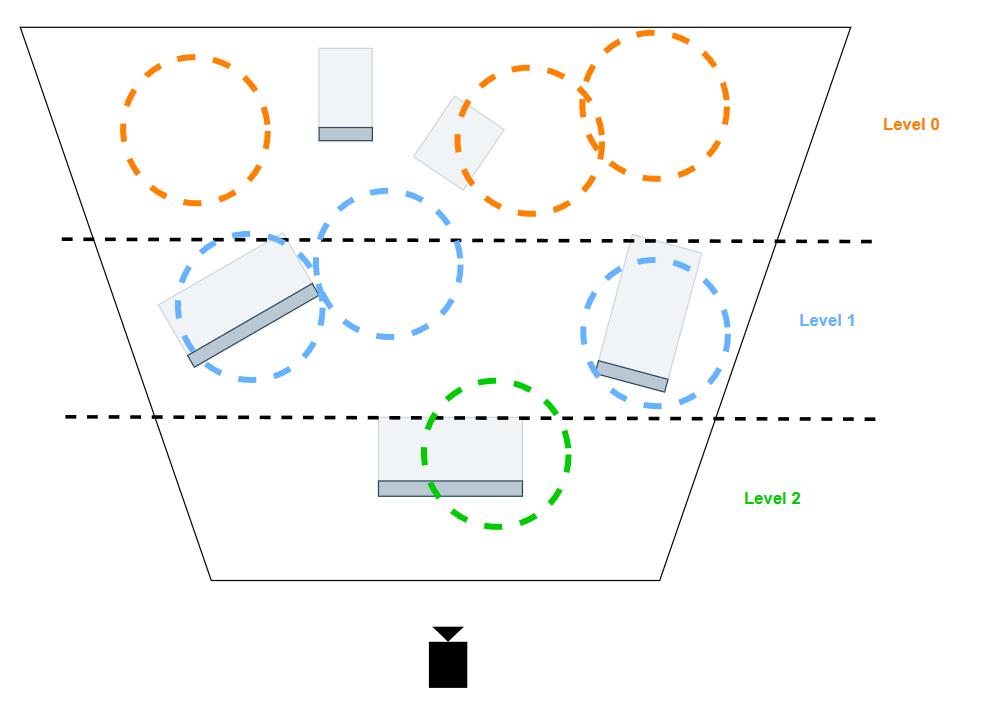
不过，分层方法仍然可能有小部分信息重叠现象（导致overdraw），但是远比 naive 的方法要少的多，同时也能将 draw call 数量从 O(n) 降为 O(m），是本人觉得比较理想的方案。

相交检测优化

大多数的光源都属于 point light/spot light，因此 tile-based lighting culling 会存在大量的 sphere- frustum 相交检测，下面就大概列举下优化的点。

这部分内容主要参考这个博客 Improve Tile-based Light Culling with Spherical-sliced Cone

Sphere-Frustum Test

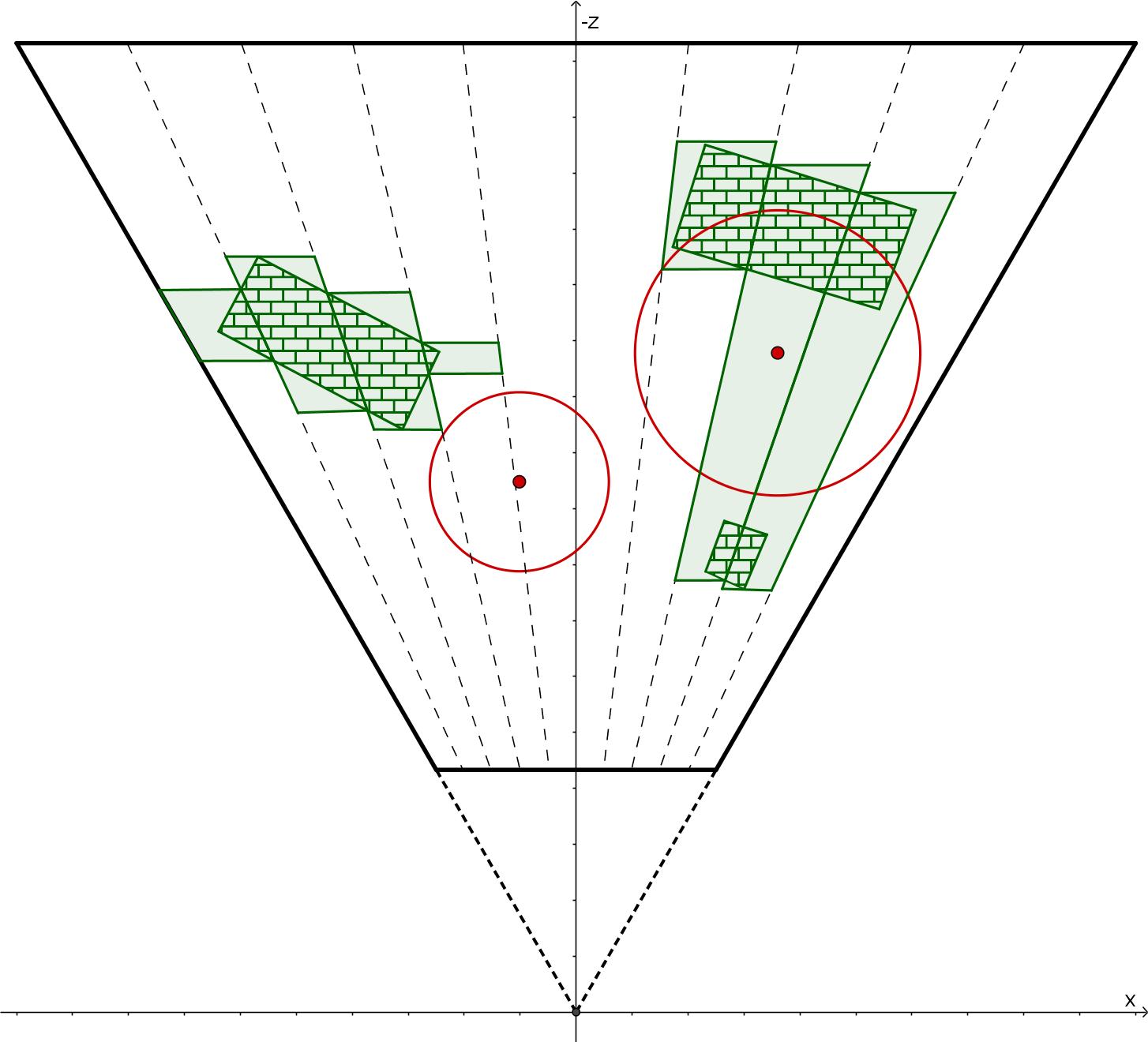
如下图，绿色区域为是 tile fustum 在侧面（xoz 平面）上真正可以被 light 影响的区域，称之为 true positive 。

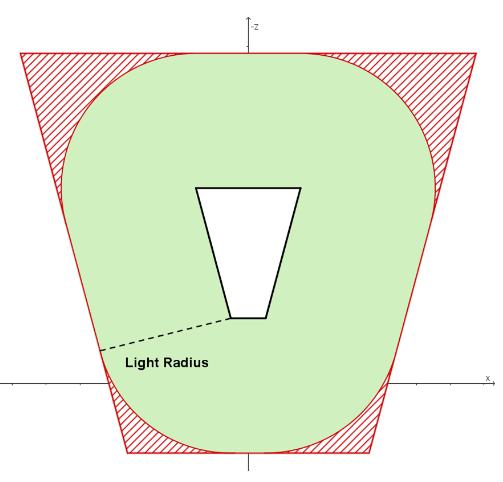
sphere-frustum test 是计算球与 frustum 的六个平面的有向距离，若有向距离均小于球半径则视为测试通过。但是，sphere- frustum 测试通过的区域会比实际区域多，多出来的部分称之为 false positive （如上图，红色区域为 false positive 区域），也是造成剔除不精细的原因。

由于 frustum 的 near&far plane 和 view 的 near&far plane 是平行的，所以在实践中往往把光源深度与 tile max depth/min depth 进行比较，这样就可以减少两个平面的有向距离计算。

// test near plane & far plane
if (lightDepth - lightRadius <= tileMaxDepth &&
    lightDepth + lightRadius >= tileMinDepth)
{
    for (int i = 0; i < 4; ++i)
    {
        // test 4 side planes
    }
}

我们的目标就是让测试产生尽可能少的 false positive，接下来我们将用 cone test 去减少 frustum 四个侧面的 test，用 spherical-slice cone test 去改进 near&far plane 的 test。

Cone Test

为了减少 false positive 区域，我们可以对 tile frustum 的 4 个侧面使用 cone test 而非 sphere-cone test。

frustum 的四个侧面在投影空间中围成一个四边形，而球体在投影空间也是一个圆，这时的问题就可以视为是 2D 空间下的四边形与圆的求交问题。如果这四个侧面仍然用 sphere-frustum test 的做法，那么 false positive 就会如下图红色部分；而 cone test 的做法是 计算出刚好包围该四边形的圆的半径，然后拿去和光源做圆与圆的相交测试 ，cone test 的 false postive 如下图的蓝色部分。

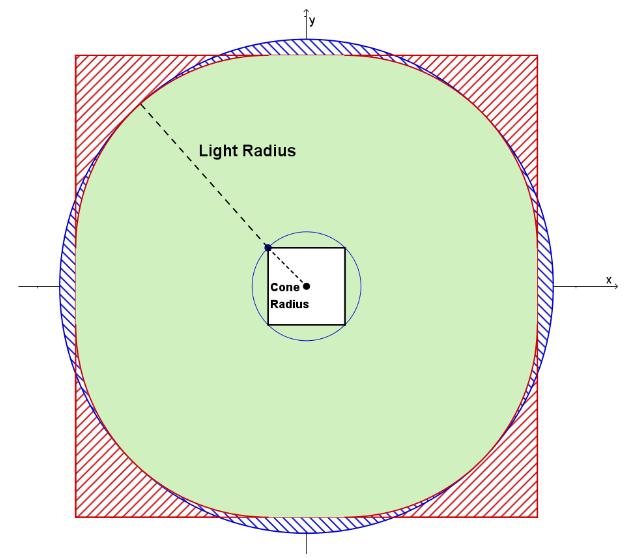
实际上，当圆远远大于四边形的时候，cone test 的 false positive（蓝色区域）会比 sphere-frustum test 的 false positive（红色区域）要更少；反之，当四边形远远大于四边形的时候，使用 sphere-cone test 会更少 false positive。

light radius 往往比 frustum 的正面四边形（面向 view 的，即 xoy 平面）要大得多，因此对于构成该四边形的四个侧面，我们可以替换成 cone test；而 frustum 的侧面四边形（xoz 或 yoz 平面）有可能因为 min/max depth 相差太大导致形状拉伸地很长，得到的 cone radius 就很大，也就不适合做 cone test。

当然在实践中，我们不用计算投影平面上的半径，而是计算 cos 值（象征着夹角大小，夹角越大cos值越小），并通过来比较光源的半角+tile的半角是否大于光源中心到 tile 中心的夹角，若是则意味着测试通过：

vec3 tileCenterVec = normalize(sides[0] + sides[1] + sides[2] + sides[3]);
float tileCos = min(min(min(dot(tileCenterVec, sides[0]), dot(tileCenterVec, sides[1])), dot(tileCenterVec, sides[2])), dot(tileCenterVec, sides[3]));
float tileSin = sqrt(1 - tileCos * tileCos);

// get lightPos and lightRadius in view space
float lightDistSqr = dot(lightPos, lightPos);
float lightDist = sqrt(lightDistSqr);
vec3 lightCenterVec = lightPos / lightDist;
float lightSin = clamp(lightRadius / lightDist, 0.0, 1.0);
float lightCos = sqrt(1 - lightSin * lightSin);

// angle of light center to tile center
float lightTileCos = dot(lightCenterVec, tileCenterVec);
float lightTileSin = sqrt(1 - lightTileCos * lightTileCos);

// special for light inside a tile
bool lightInsideTile = lightRadius > lightDist;
// sum angle = light cone half angle + tile cone half angle
// ps: cos(A+B) = cos(A)*cos(B) - sin(A)*sin(B)
float sumCos = lightInsideTile ? -1.0 : (tileCos * lightCos - tileSin * lightSin);

if (sumCos <= lightTileCos // cone test
    && lightDepth - lightRadius <= tileMaxDepth // far plane test
    && lightDepth + lightRadius >= tileMinDepth // near plane test
   )
{
    // light intersect this tile
}

Spherical-sliced Cone Test

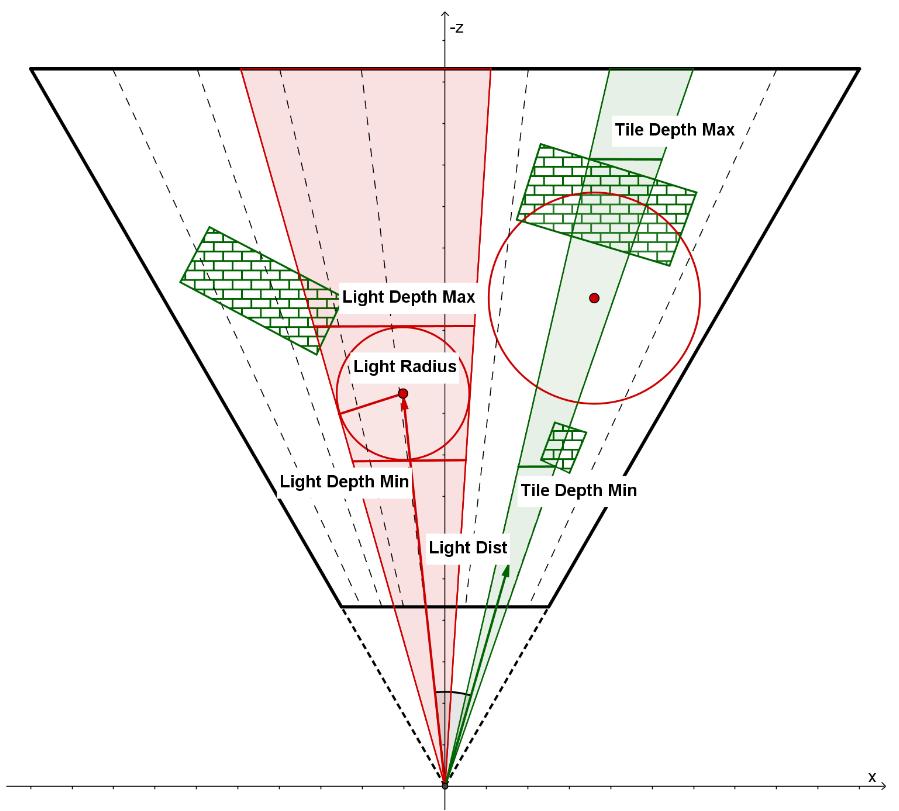
对于 frustum 的 near&far plane，传统的 sphere-frusutm test 只基于深度去判断，会导致相当多的 false positive（如下图左侧）；而 spherical-sliced cone test 则基于距离去判断，并且还考虑了投影在距离轴上的实际 min&max 范围，具有更好的 culling 效率（如下图右侧）。

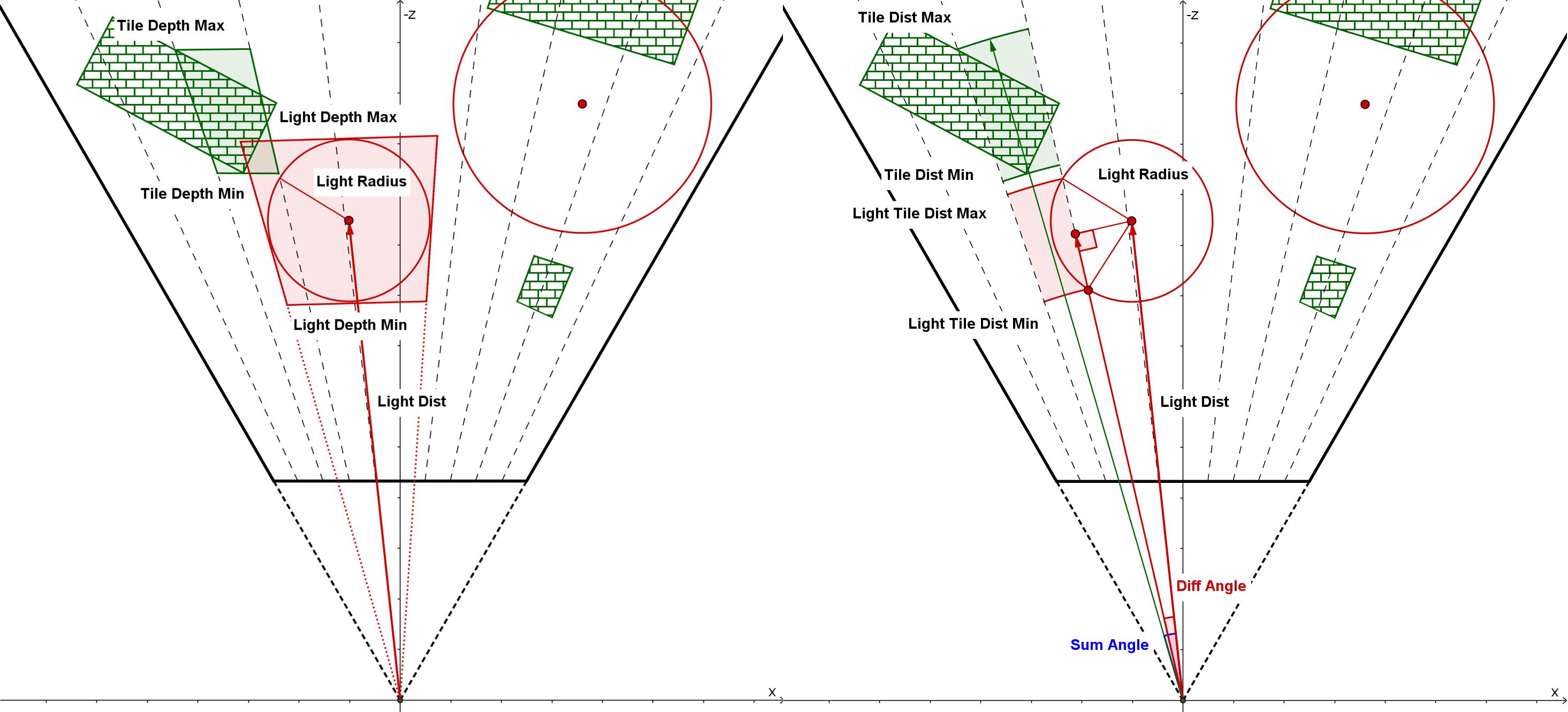
Spherical-sliced Cone Test 的大概做法是算出 light 中心投影在距离轴上的位置（lightTileDistBase）和 light 半径投影在距离轴上的长度（lightTileDistOffset），从而确定了 min&max dist 的范围：

ps：因为 spherical-sliced cone test 是基于距离的，因此 tile 被视为一个切过片的圆，从而能更容易做 light 投影到 tile 距离轴的计算；至于基于深度的方式，要投影到深度轴则计算困难得多，且 culling 效率也不如距离轴。

// diff angle = sum angle - tile cone half angle
// clamp to handle the case when light center is within tile cone
float diffSin = clamp(lightTileSin * tileCos - lightTileCos * tileSin, 0.0, 1.0);
float diffCos = (diffSin == 0.0) ? 1.0 : lightTileCos * tileCos + lightTileSin * tileSin;
float lightTileDistOffset = sqrt(lightRadius * lightRadius - lightDistSqr * diffSin * diffSin);
float lightTileDistBase = lightDist * diffCos;

if (lightTileCos >= sumCos &&
    lightTileDistBase - lightTileDistOffset <= maxTileDist &&
    lightTileDistBase + lightTileDistOffset >= minTileDist)
{
    // light intersect this tile
}

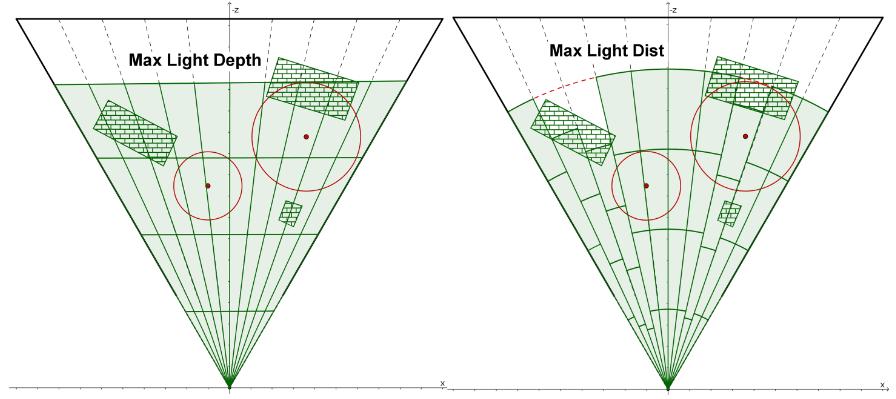
如图分别为：(a) 正常渲染； (b) 通过 sphere-frustum test 的 tiles； © 通过 cone test 的 tiles； (d) 通过 cone test + spherical-sliced cone test 的 tiles；

| Lighting Time | Improvement

Sphere-Frustum Test(6 planes)	5.55 ms	0%
Cone Test(4 side planes) + Sphere-Frustum Test(near &far planes)	5.30 ms	4.50%
Cone Test(4 side planes) + Spherical-sliced Cone Test(near &far planes)	4.68 ms	15.68%

UnrealEngine 5.1 多光源源码剖析

Cluster-based Light Culling

light culling，每个 cluster（在 UE5.1 里被称为 grid）在屏幕上占据 64 × 64 pixels，在 z 轴上默认分成 32 个 slices。

相交检测 ：

• 在 view space 进行 sphere-AABB test：对 cluster 从 clip space 的 AABB 变换到 view space 下的六面体，并再建立新的 AABB 包围住该六面体；最后让该 AABB 与 point light 进行 sphere-AABB test。

• 针对 spot light 的 cone-AABB test：对 cluster 从 clip space 的 AABB 变换到 view space 下的六面体，并再建立新的 AABB 包围住该六面体；然后构建一个贴在 spot light cone 上的平面，并且这个平面正对着 AABB 中心；最后让该平面与 AABB 进行 plane-AABB test。

UE5.1 的相交检测其实大有优化空间，因为建立新的 AABB 会导致 cluster 的额外扩展，造成很多 false positive 以及带来的 culling 效率下降。

culling 数据结构的构建 ：

• 可以选择均匀空间的 cluster light index 数组：
  • 省去了 compact pass。
  • 占据更多显存空间（而且绝大部分是被浪费的）。
  • 某些地方极端多光源的情况下，部分 tile 会发生光源截断（即不能容纳所有的光源）。
• 可以选择基于 Linked List 的 culling 流程：
  • LDS（local data share）优化：先利用 group shared 组成局部 linked list，然后再组成全局 linked list。

UE 5.1 culling 数据结构的构建：LightGridInjection.usf 和 LightGridCommon.ush。

UE 5.1 很多渲染流程都在最终 shading 用到了 light culling：

• 前向渲染：默认启动 cluster-based light culling；shader 代码见 ForwardLightingCommon.ush。
• 延迟渲染管线： 需启用 r.UseClusteredDeferredShading ；shader 代码见 MobileDeferredShading.usf。
• mobile 延迟渲染管线：需启用 r.Mobile.UseClusteredDeferredShading；shader 代码见 ClusteredDeferredShadingPixelShader.usf。

Draw Light Volume

使用了基于 depth bounds test 的方法，并且将同类光源进行批量处理（对应于 batched lights），减少 PSO（pipeline state object） 切换的开销。但也存在一些无法批处理的光源（unbatched lights），例如包含 shadow map 的光源。不过，UE 没有使用 instancing 优化方式，这点存在改进空间。

更多 idea

相交检测优化

• 在 GPU 里进行光源相交检测前，最好先在 CPU 层面对光源进行粗粒度的视锥体剔除，以避免将大部分无关光源上传到 GPU 里。
• 可以将优化的相交检测同样应用到 cluster-based light culling 上：

• 对于 spot light 这种锥形的形状进行 culling 的算法可能是费时的，可以考虑用球包围盒将其锥形包住，并将其视为 sphere 进行与 point light 一样的 culling 处理。当然球包围盒可以在 CPU 端预先计算出来，这样传递给 GPU 将可以统一成对 sphere 处理的 shader 代码。

  float spotLightConeHalfAngleCos = cos(spotLightFOV * 0.5f); float sphereRadius = spotlightRange * 0.5f / (spotLightConeHalfAngleCos *spotLightConeHalfAngleCos); float3 sphereCenter = spotLightPos + spotLightDirection * sphereRadius;

当然也可以探索锥形形状的 culling 算法，例如有涉及 cone-sphere test 的文章: “Cull that Cone”。

Light Culling 相关结构的优化

• 面对千万级的光源数量，填充 culling 数据结构的流程本身就需要遍历太多光源，相当耗费性能，可以分层次剔除，并且越大的层次 test 粒度可以越粗：先用大块 tile 进行粗粒度 test（例如八叉树），再用小块 tile 进行细粒度 test 。
• sorted lights：在 CPU 就根据光源类型排序好光源，从而让 shader 减少类型判断代码，针对同一类型的光源批量处理。
• 对于静态光源可以建立具有滚动优化的 light grid 结构，并且一般 grid 粒度更细；对于动态光源则建立正常 light grid 结构，一般 grid 粒度更粗。

滚动优化：新 grid 在上一帧结构找到原位时，直接复制原 grid 的光源列表到新的光源列表；否则，再对全局光源列表进行遍历检测相交来添加到新的光源列表。

• async compute 优化：shadow map passes 的 pixel shader 基本无ALU计算，属于带宽负载型任务，且还使用光栅化硬件；而 light culling pass 是计算负载型任务，也不需要用到光栅化引擎。这两类任务之间没有任何数据依赖关系，因此可以将这两类 pass 进行异步，充分利用 GPU 硬件。

Light Culling in GI

• light culling 往往用于 view frustum 内的 direct lighting shading，而 view frustum 之外就没有 culling 数据结构；因此如果要将 light culling 的思想应用于 GI，就需要建立另一套 culling 数据结构以囊括 view frustum 之外的空间（GI 仍有可能需要在 view frustum 内搜集 direct lighting，这时候也可以选择复用传统的 culling 数据结构，在 view frustum 之外则 fall back 成别的 culling 结构）。

Battlefield V 就使用了囊括 camera 周围空间（而非只覆盖 view frustum）的 grid-based light culling，并同样使用 linked list 作为实际数据结构；此外由于该游戏地图大部分在一个地面上，因此在高度轴上可以不进行划分（即 grid.dimension.y = 1），减少 grid 的总数。

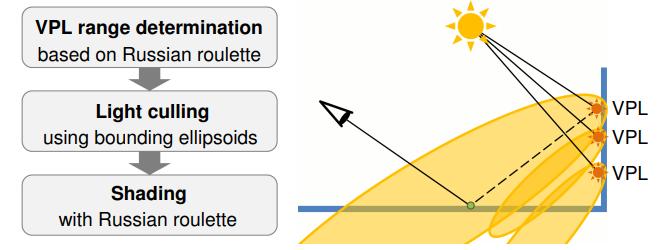
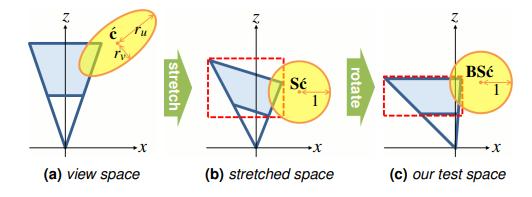
• 基于 VPL（virtual point light） specular lobe 的 light culling：将 VPL 视为光源，根据它们的 specular lobe 来构造椭圆包围盒，并通过 russian roulette 来随机决定 lobe 的长度（避免因 culling 造成的能量截断）。通过 stretch 和 rotate 来做椭圆和 frustum 的相交检测。

Normal-based Light Culling

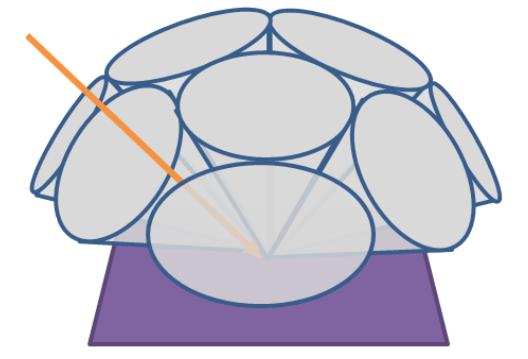
除了 tile 和 cluster 这种基于空间分布（二维空间和三维空间）来 culling 光源的，我们还可以额外再扩展出基于法线的分布，用于剔除背向的光源。例如，可以用一堆均匀排布且半角相同的 cone 来表示不同的法线范围。此外，为了包住所有球面方向，相邻的 cone 之间必定有范围重叠。

下图不太准确，因为只是大概提供了包住半球方向的一些 cone，并且 cone 之间有空隙，仅用于直观理解 cone 如何均匀排布。

这样，我们就可以先根据每个光源的朝向，填充光源到对应 cone 的光源列表中，在 shading 时通过计算 shading point 的法线归属于第几个 cone 来快速找到对应的光源列表。

实际上，normal-based light culling 往往是结合 tile 或 cluster 一起使用，其实就是额外扩展多一个维度用于索引光源列表。原本仅通过位置得到的 3D 索引(x, y, z) 现在可以变成 4D 索引（x, y, z, normal）。

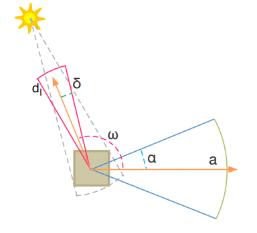
\(\alpha\) 是一个法线分布的 cone 半角，\(\delta\) 则是光源的半角（directional light 为 0，point light 为 \(\frac{\pi}{4}\)，spot light 为指定半角）；cone 的中心方向记为 \(\mathrm{a}\) ，光源的反向向量记为 \(\mathrm{d_l}\) 。

• culling 数据结构的构建，对每个 cone：遍历光源，如果光源反向向量 \(\mathrm{d_l}\) 与 cone 的中心方向 \(\mathrm{a}\) 的夹角 \(\omega < \frac{\pi}{2}+\alpha+\delta\) ，那么光源添加进该 cone 的光源列表。
• 最终 shading：直接通过 shading point 的法线计算出 cone 索引，并获取该 cone 的光源列表。

参考

• Improve Tile-based Light Culling with Spherical-sliced Cone | Eric’s Blog
• A 2.5D CULLING FOR FORWARD+ | SIGGRAPH ASIA 2012
• Optimizing tile-based light culling | Wicked Engine Net
• 《GPU Pro 7: Advanced Rendering Techniques》
• It Just Works: Ray-Traced Reflections in “Battlefield V” | GDC 2019
• Stochastic Light Culling for VPLs on GGX Microsurfaces [Tokuyoshi 2017]
• 游戏引擎中的渲染管线 - 知乎 (zhihu.com)
• Fine Pruned Tiled Light | wingstone’s blog