《深度学习入门·基于Python的理论与实现》代码笔记

花了4天看完了《深度学习入门·基于Python的理论与实现》这本书 然后用一天时间自己试着实现了一下这里面的代码

其中后面深层卷积神经网络的部分有点难 我尝试着实现了一下结果发现有好多bug 由于马上要开始复习期末考试了就不继续深究了 今天就是寒假弄这个的最后一天 写个随笔记录一下 之后就好好复习了

代码部分关键的地方我都放了注释所以文章就不提具体实现了 前面看一下几个运行的结果和反映出来的一些现象 后面放源代码 之后相关的一些文件包括全书pdf也会放在博客里面

水平很差 如果有问题欢迎批评指正!

目录

• 实验数据与现象
  • TwoLayerNet_Numerical类
  • TwoLayerNet_BackPropagation类
  • MultiLayerNet类
• 源代码
  • mnist.py
  • main.py

实验数据与现象

TwoLayerNet_Numerical类

• 使用的是数值微分梯度下降

• 学习10次 时间五分半 太耗时了 所以这个数值微分只能用来进行梯度验证的时候用一下

• 

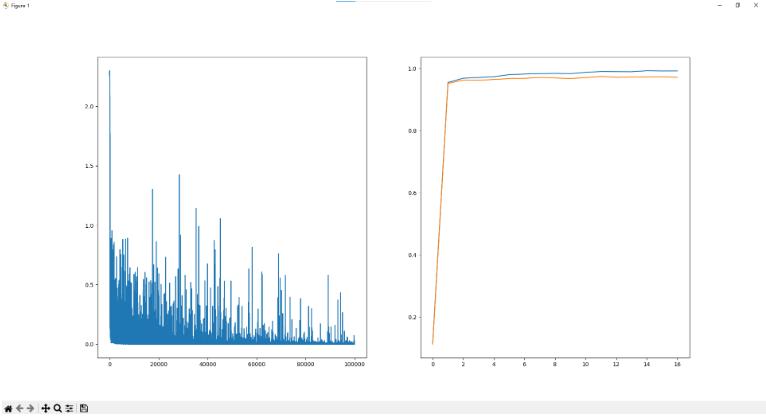
TwoLayerNet_BackPropagation类

• 用反向传播法求了梯度 学习100000次 仅仅耗时了一分半 显著提高效率 结果上 训练集准确率达到99.3% 测试集准确率97.1%

• 

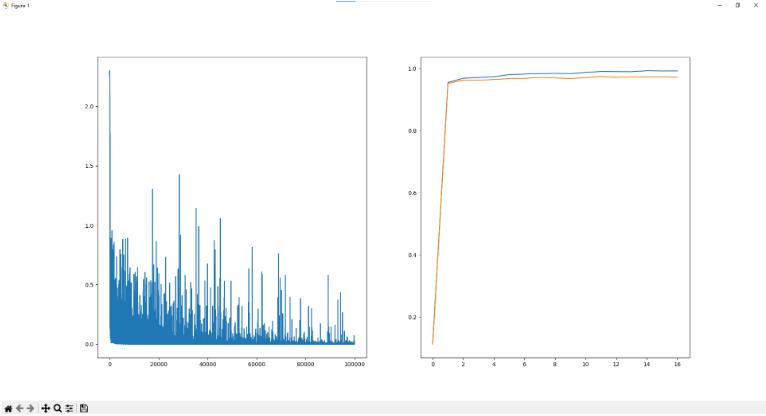
MultiLayerNet类

• 多层神经网络 因为模块化 所以可以任意更改中间隐藏层的大小 上面的两个TwoLayerNet类只是用来练习用的 之后详细扩展就需要这种可拓展性比较好的实现

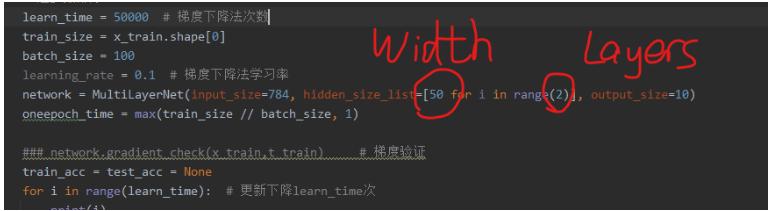
其中Width是隐藏层神经元的个数 Layers是隐藏层的层数

• 不同的层数 最终学习情况如下:

  • 2层网络

学习50000次 耗时:157.87秒

训练集准确率为97.11% 验证集准确率为96.63%

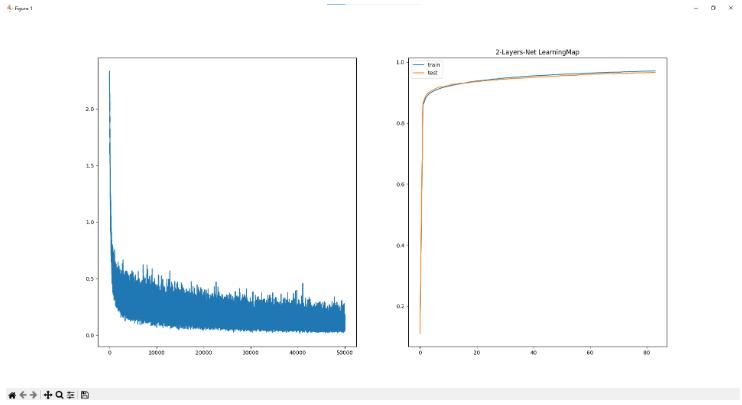
* 3层网络

学习50000次 耗时:182.40秒

训练集准确率为98.58% 验证集准确率为97.17%

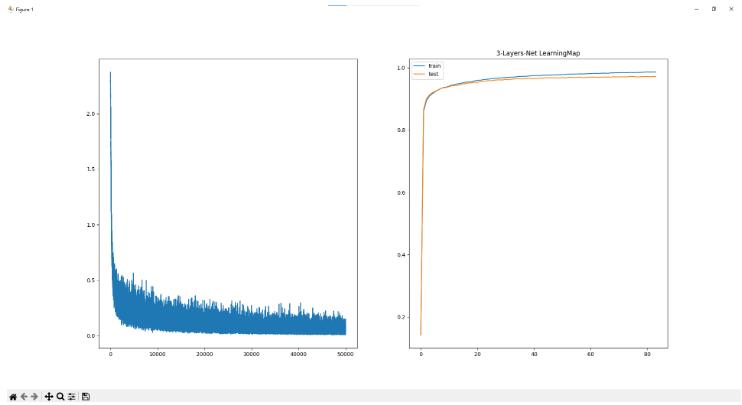
* 4层网络

学习50000次 耗时:194.60秒

训练集准确率为99.34% 验证集准确率为97.36%

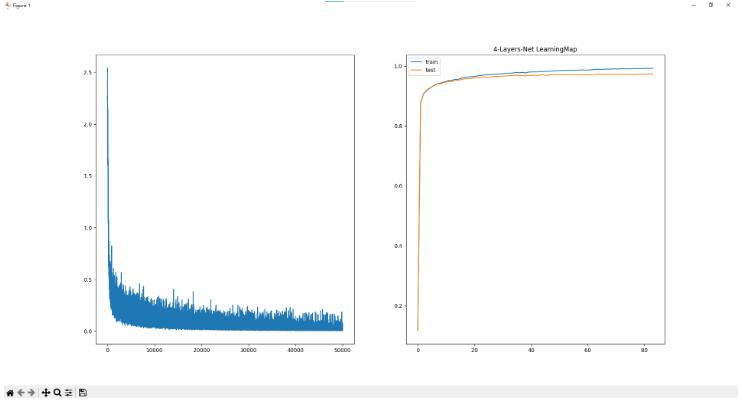
* 8层网络

学习50000次 耗时:285.70秒

训练集准确率为99.96% 验证集准确率为96.78%

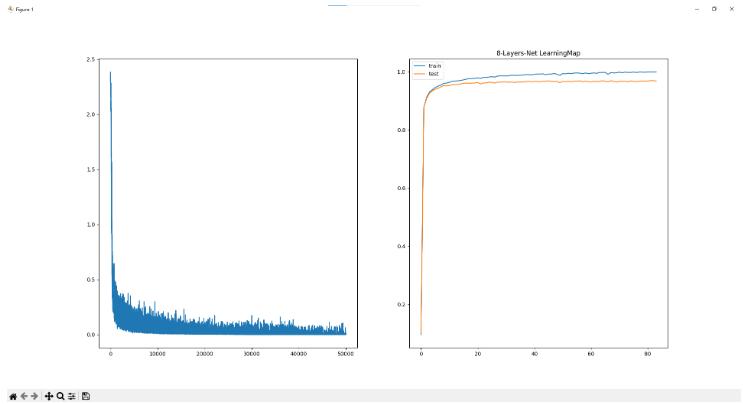
* 16层网络

学习50000次 耗时:448.04秒

训练集准确率为99.67% 验证集准确率为96.76%

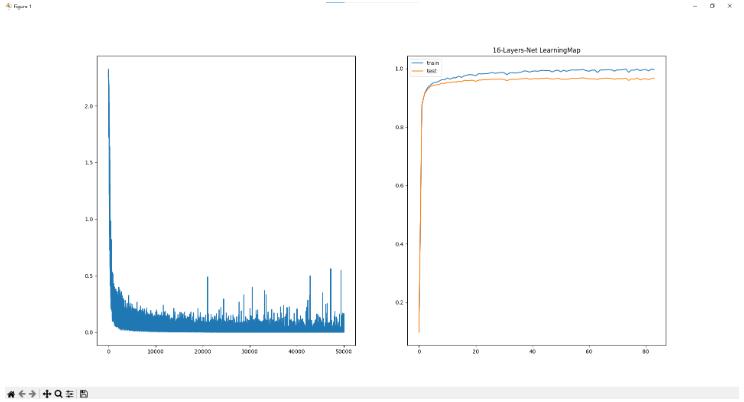
* 32层网络

学习50000次 耗时:703.78秒

训练集准确率为99.46% 验证集准确率为96.68%

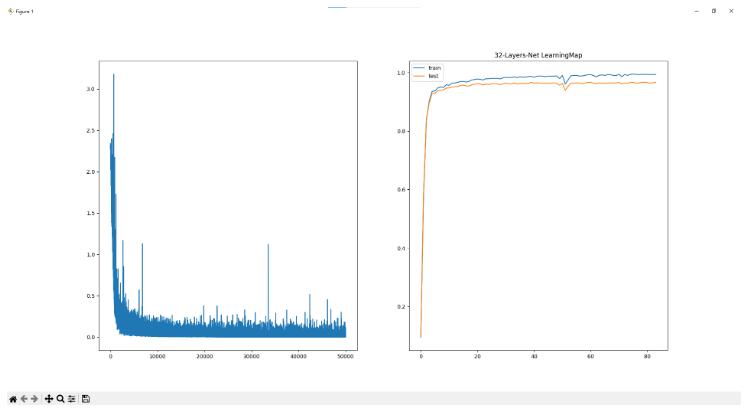
* 50层网络

学习50000次 耗时:969.98秒

训练集准确率为9.87% 验证集准确率为9.80% (??? 炸了?????)

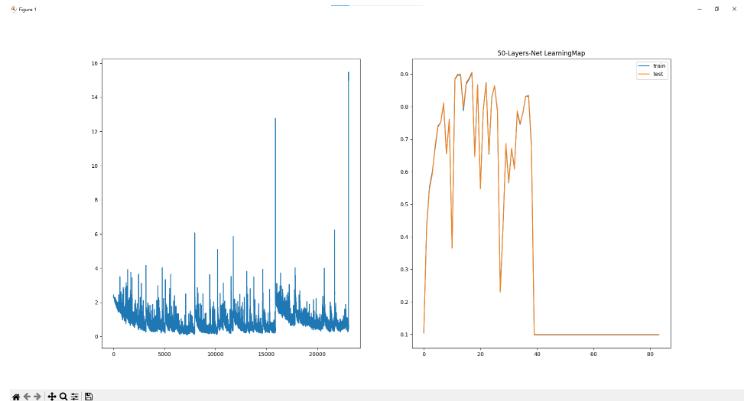
* 64层网络

学习50000次 耗时:1269.11秒

训练集准确率为52.07% 验证集准确率为53.25%

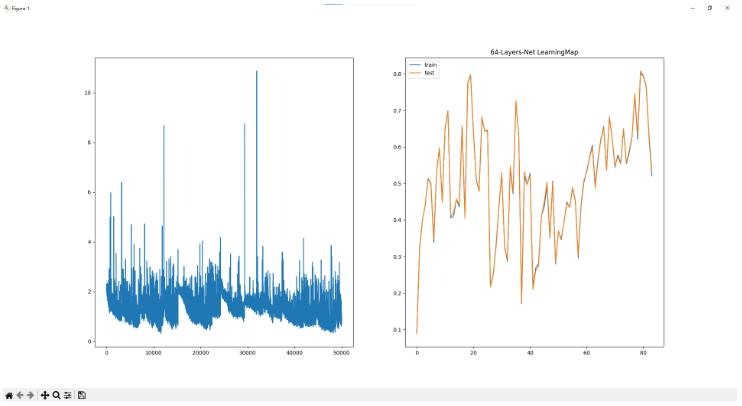
• 很显然 层数太大了之后 爆炸了

有可能是隐藏层的总参数太多 导致有一些神经元在学习的过程中死亡了 最终导致结果的崩盘

抛开爆炸的那些不谈 能够发现随着层数的增加 训练集的准确率慢慢的和验证集准确率越分越远 也就是说慢慢的有过拟合的问题出现了 如果训练集的数据不是60000组而是600组 那这个问题就会非常明显了

我们将训练集调整为600组 学习次数50000次 层数为5层 mini-batch大小设置为10 尝试一下:

3层网络 学习50000次 耗时:111.24秒 训练集准确率为100.00% 验证集准确率仅为86.13%

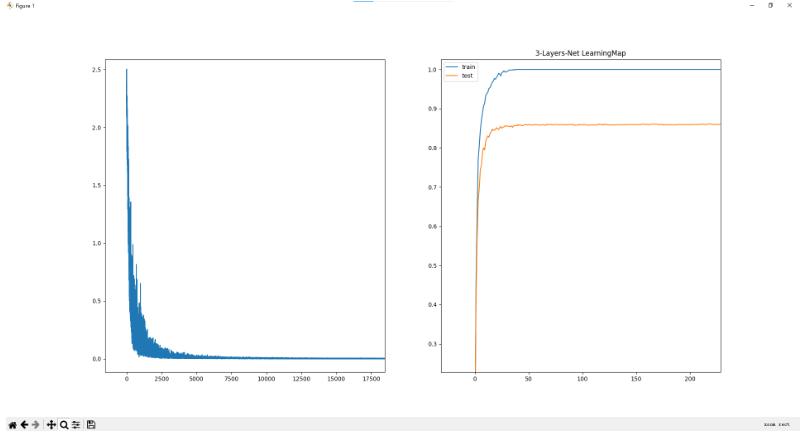
这个很显然是发生了过拟合情况

• 为了解决过拟合 可以在我们MultiLayerNet类的实现里面的loss函数 增添正则化参数 (λ*W^2)/2

添加之后我们再查看一下学习情况:

3层网络 学习50000次 耗时:209.86秒 训练集准确率为100.00% 验证集准确率为92.76%

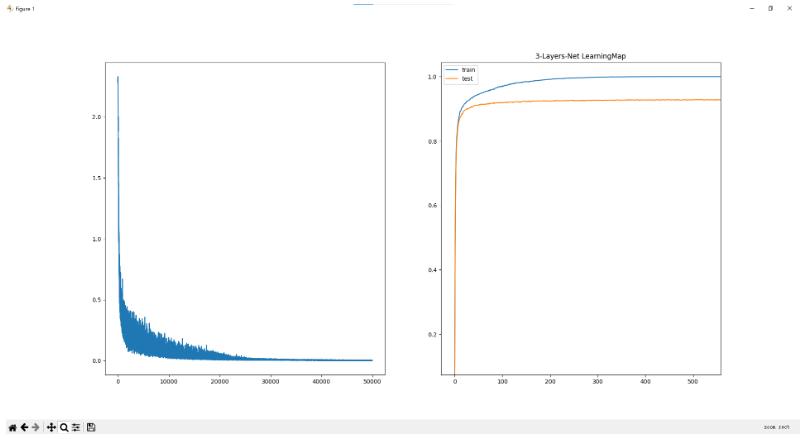
能够发现过拟合的问题虽然还是有 但是好了很多 测试集的准确率也上升了不少 说明正则化还是有效的

源代码

下面就是源代码部分 其中mnist.py是直接偷过来的 用处是获取mnist数据集 main.py就是自己看书实现的一些神经网络

mnist.py

# coding: utf-8

# 这个读取mnist的程序是纯拿过来用的  所以具体实现也不是很会
try:
    import urllib.request
except ImportError:
    raise ImportError('You should use Python 3.x')
import os.path
import gzip
import pickle
import os
import numpy as np

url_base = 'http://yann.lecun.com/exdb/mnist/'
key_file = {
    'train_img': 'train-images-idx3-ubyte.gz',
    'train_label': 'train-labels-idx1-ubyte.gz',
    'test_img': 't10k-images-idx3-ubyte.gz',
    'test_label': 't10k-labels-idx1-ubyte.gz'
}

dataset_dir = os.path.dirname(os.path.abspath(__file__))
save_file = dataset_dir + "/mnist.pkl"

train_num = 60000
test_num = 10000
img_dim = (1, 28, 28)
img_size = 784


def _download(file_name):
    file_path = dataset_dir + "/" + file_name

    if os.path.exists(file_path):
        return

    print("Downloading " + file_name + " ... ")
    urllib.request.urlretrieve(url_base + file_name, file_path)
    print("Done")


def download_mnist():
    for v in key_file.values():
        _download(v)


def _load_label(file_name):
    file_path = dataset_dir + "/" + file_name

    print("Converting " + file_name + " to NumPy Array ...")
    with gzip.open(file_path, 'rb') as f:
        labels = np.frombuffer(f.read(), np.uint8, offset=8)
    print("Done")

    return labels


def _load_img(file_name):
    file_path = dataset_dir + "/" + file_name

    print("Converting " + file_name + " to NumPy Array ...")
    with gzip.open(file_path, 'rb') as f:
        data = np.frombuffer(f.read(), np.uint8, offset=16)
    data = data.reshape(-1, img_size)
    print("Done")

    return data


def _convert_numpy():
    dataset = {}
    dataset['train_img'] = _load_img(key_file['train_img'])
    dataset['train_label'] = _load_label(key_file['train_label'])
    dataset['test_img'] = _load_img(key_file['test_img'])
    dataset['test_label'] = _load_label(key_file['test_label'])

    return dataset


def init_mnist():
    download_mnist()
    dataset = _convert_numpy()
    print("Creating pickle file ...")
    with open(save_file, 'wb') as f:
        pickle.dump(dataset, f, -1)
    print("Done!")


def _change_one_hot_label(X):
    T = np.zeros((X.size, 10))
    for idx, row in enumerate(T):
        row[X[idx]] = 1

    return T


def load_mnist(normalize=True, flatten=True, one_hot_label=False):
    """读入MNIST数据集

    Parameters
    ----------
    normalize : 将图像的像素值正规化为0.0~1.0
    one_hot_label :
        one_hot_label为True的情况下，标签作为one-hot数组返回
        one-hot数组是指[0,0,1,0,0,0,0,0,0,0]这样的数组
    flatten : 是否将图像展开为一维数组

    Returns
    -------
    (训练图像, 训练标签), (测试图像, 测试标签)
    """
    if not os.path.exists(save_file):
        init_mnist()

    with open(save_file, 'rb') as f:
        dataset = pickle.load(f)

    if normalize:
        for key in ('train_img', 'test_img'):
            dataset[key] = dataset[key].astype(np.float32)
            dataset[key] /= 255.0

    if one_hot_label:
        dataset['train_label'] = _change_one_hot_label(dataset['train_label'])
        dataset['test_label'] = _change_one_hot_label(dataset['test_label'])

    if not flatten:
        for key in ('train_img', 'test_img'):
            dataset[key] = dataset[key].reshape(-1, 1, 28, 28)

    return (dataset['train_img'], dataset['train_label']), (dataset['test_img'], dataset['test_label'])


if __name__ == '__main__':
    init_mnist()

main.py

import os
import sys
import numpy as np

sys.path.append(os.pardir)
from mnist import load_mnist  # 获取mnist数字图像数据集
from PIL import Image  # 显示mnist数据用
from matplotlib import pyplot as plt  # 画函数图像
import time
from collections import OrderedDict


# 显示mnist数据图像
def img_show(img):
    img = img.reshape(28, 28)
    if type(img[0][0]).__name__ == 'float32':  # 如果进行了正规化 则乘255变为int形式
        img *= 255.0
    pil_img = Image.fromarray(np.uint8(img))  # 将img矩阵的每一个像素转换为8位int  并通过转换函数转换为Image类型
    pil_img.show()


# 激活函数
## sigmoid
def sigmoid(x):
    return 1.0 / (1.0 + np.exp(-x))  # 没有分母为0的可能 所以不用加保护量


## ReLU
def relu(x):
    return np.maximum(x, 0)  # x>0就返回x x<0就返回0


# 代价函数
## 均方误差
def mean_square_error(y, t):
    return np.sum((y - t) ** 2) / 2.0  # ans = sum((y-t)^2)/2


## 交叉熵误差(mini-batch版本)
def cross_entropy_error(y, t):
    if y.ndim == 1:  # 输出数组的维数是1  那么需要转换一下形状以确保统一
        t = t.reshape(1, t.size)
        y = y.reshape(1, y.size)

    # 监督数据是one-hot-vector的情况下，转换为正确解标签的索引
    if t.size == y.size:
        t = t.argmax(axis=1)  # 提取出每一行最大值  即把向量形式的监督值转换为数字形式

    batch_size = y.shape[0]
    return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size  # 注意这里面加了一个1e-7以防出现log(0)


#  还有一个注意事项: 原版的交叉熵是要求和 而我们的mnist数据集的t监督向量只有一个是1  所以也不需要求和了 找到对应的那个y值放进log就行


# 数值微分求梯度
def numerical_gradient(f, x):
    dx = 1e-4;  # 数值微分的小微元dx
    grads = np.zeros_like(x)  # 生成和x一样大小的梯度向量 等待填入计算结果
    if x.ndim == 2:
        xshape_x = x.shape[1]
        for idx in range(x.size):
            idx_x = idx // xshape_x
            idx_y = idx % xshape_x
            temp = x[idx_x][idx_y]  # 临时存储idx处的x值
            x[idx_x][idx_y] = temp + dx
            f1 = f(x)
            x[idx_x][idx_y] = temp - dx
            f2 = f(x)
            grads[idx_x][idx_y] = (f1 - f2) / (2 * dx)
            x[idx_x][idx_y] = temp  # 还原x
        return grads
    if x.ndim == 1:
        for idx in range(x.size):
            temp = x[idx]  # 临时存储idx处的x值
            x[idx] = temp + dx
            f1 = f(x)
            x[idx] = temp - dx
            f2 = f(x)
            grads[idx] = (f1 - f2) / (2 * dx)
            x[idx] = temp  # 还原x
        return grads


# 神经网络各层的实现
## Sigmoid层
class Sigmoid:
    def __init__(self):
        self.out = None

    def forward(self, x):  # 前向
        out = self.out = sigmoid(x)  # 最好返回一个新的变量  不然可能会导致类的封装性受损
        return out

    def backward(self, dout):  # 反向
        dx = dout * (1.0 - self.out) * self.out  # 反向传播在传过来的dout基础上乘上y(1-y)
        return dx


## Relu层
class Relu:
    def __init__(self):
        self.mask = None

    def forward(self, x):
        self.mask = (x <= 0)
        out = x.copy()  # 注意python变量赋值自动算作是引用 这里不能更改x所以要copy它
        out[self.mask] = 0
        return out

    def backward(self, dout):
        dout[self.mask] = 0
        dx = dout
        return dx


## Affine层
class Affine:
    def __init__(self, w, b):  # 构造函数传入该层的权重w和偏置b
        self.out = None
        self.w = w
        self.b = b
        self.original_x_shape = None
        self.x = None
        self.dx = None  #
        self.dw = None  # 这两个是反向传播过来的梯度大小

    def forward(self, x):
        # 对应张量
        self.original_x_shape = x.shape
        x = x.reshape(x.shape[0], -1)
        self.x = x
        out = np.dot(self.x, self.w) + self.b
        return out

    def backward(self, dout):
        dx = np.dot(dout, self.w.T)  # dx = dout * w'
        self.dw = np.dot(self.x.T, dout)  # dw = x' * dout
        self.db = np.sum(dout, axis=0)  # db = dout 在 竖直方向的求和
        dx = dx.reshape(*self.original_x_shape)  # 还原输入数据的形状（对应张量）
        return dx


## Softmax输出层
def softmax(x):
    if x.ndim == 2:
        x = x.T
        x = x - np.max(x, axis=0)
        y = np.exp(x) / np.sum(np.exp(x), axis=0)
        return y.T
    x = x - np.max(x)  # 溢出对策 调整参数防止e^x过大
    return np.exp(x) / np.sum(np.exp(x))


class SoftmaxWithLoss:
    def __init__(self):
        self.loss = None
        self.y = None  # 输出数据
        self.t = None  # 监督数据 即正确答案 毕竟输出层需要给出代价函数

    def forward(self, x, t):
        self.t = t
        self.y = softmax(x)  # 使用softmax进行标准化
        loss = self.loss = cross_entropy_error(self.y, self.t)  # 使用交叉熵误差来计算代价函数
        return loss

    def backward(self, dout=1):  # 因为是最后一层  所以dout通常是1
        batch_size = self.t.shape[0]
        dx = (self.y - self.t) / batch_size  # 这里有个minibatch的调整
        return dx


## Dropout层
class Dropout:
    def __init__(self, dropout_ratio=0.5):
        self.dropout_ratio = dropout_ratio  # 将几成比例的神经元给忽略静默掉
        self.mask = None

    def forward(self, x, train_flg=True):
        if train_flg:
            self.mask = np.random.rand(*x.shape) > self.dropout_ratio
            # 注意这里是rand而不是randn  因为需要的是均匀分布的随机数 而非高斯分布
            return x * self.mask
        else:
            return x * (1.0 - self.dropout_ratio)  # 如果flg是False  注意这里是如何前向传播的

    def backward(self, dout):
        return dout * self.mask  # mask不变 前后项一样


# 卷积神经网络各层的实现
## im2col和col2im函数实现(书中提供的实现)
def im2col(input_data, filter_h, filter_w, stride=1, pad=0):
    """

    Parameters
    ----------
    input_data : 由(数据量, 通道, 高, 长)的4维数组构成的输入数据
    filter_h : 滤波器的高
    filter_w : 滤波器的长
    stride : 步幅
    pad : 填充

    Returns
    -------
    col : 2维数组
    """
    N, C, H, W = input_data.shape
    out_h = (H + 2 * pad - filter_h) // stride + 1
    out_w = (W + 2 * pad - filter_w) // stride + 1

    img = np.pad(input_data, [(0, 0), (0, 0), (pad, pad), (pad, pad)], 'constant')
    col = np.zeros((N, C, filter_h, filter_w, out_h, out_w))

    for y in range(filter_h):
        y_max = y + stride * out_h
        for x in range(filter_w):
            x_max = x + stride * out_w
            col[:, :, y, x, :, :] = img[:, :, y:y_max:stride, x:x_max:stride]

    col = col.transpose(0, 4, 5, 1, 2, 3).reshape(N * out_h * out_w, -1)
    return col


def col2im(col, input_shape, filter_h, filter_w, stride=1, pad=0):
    """

    Parameters
    ----------
    col :
    input_shape : 输入数据的形状（例：(10, 1, 28, 28)）
    filter_h :
    filter_w
    stride
    pad

    Returns
    -------

    """
    N, C, H, W = input_shape
    out_h = (H + 2 * pad - filter_h) // stride + 1
    out_w = (W + 2 * pad - filter_w) // stride + 1
    col = col.reshape(N, out_h, out_w, C, filter_h, filter_w).transpose(0, 3, 4, 5, 1, 2)

    img = np.zeros((N, C, H + 2 * pad + stride - 1, W + 2 * pad + stride - 1))
    for y in range(filter_h):
        y_max = y + stride * out_h
        for x in range(filter_w):
            x_max = x + stride * out_w
            img[:, :, y:y_max:stride, x:x_max:stride] += col[:, :, y, x, :, :]

    return img[:, :, pad:H + pad, pad:W + pad]


## 卷积层
class Convolution:
    def __init__(self, w, b, stride=1, pad=0):
        self.w = w
        self.b = b
        self.stride = stride
        self.pad = pad

        # 中间数据（backward时使用）
        self.x = None
        self.col = None
        self.col_w = None

        self.dw = None
        self.db = None

    def forward(self, x):
        FN, C, FH, FW = self.w.shape
        N, C, H, W = x.shape
        out_h = 1 + int((H + 2 * self.pad - FH) / self.stride)
        out_w = 1 + int((W + 2 * self.pad - FW) / self.stride)  # 计算出卷积之后的结果形状

        col = im2col(x, FH, FW, self.stride, self.pad)  # Image to Column  将输入数据展开
        col_w = self.w.reshape(FN, -1).T

        out = np.dot(col, col_w)
        out += self.b
        out = out.reshape(N, out_h, out_w, -1).transpose(0, 3, 1, 2)

        self.x = x
        self.col = col
        self.col_w = col_w

        return out

    def backward(self, dout):
        FN, C, FH, FW = self.w.shape
        dout = dout.transpose(0, 2, 3, 1).reshape(-1, FN)

        self.db = np.sum(dout, axis=0)
        self.dw = np.dot(self.col.T, dout)
        self.dw = self.dw.transpose(1, 0).reshape(FN, C, FH, FW)

        dcol = np.dot(dout, self.col_w.T)
        dx = col2im(dcol, self.x.shape, FH, FW, self.stride, self.pad)

        return dx


## 池化层
class Pooling:
    def __init__(self, pool_h, pool_w, stride=1, pad=0):
        self.pool_h = pool_h
        self.pool_w = pool_w
        self.stride = stride
        self.pad = pad

        self.x = None
        self.arg_max = None

    def forward(self, x):
        N, C, H, W = x.shape
        out_h = int(1 + (H - self.pool_h) / self.stride)
        out_w = int(1 + (W - self.pool_w) / self.stride)

        col = im2col(x, self.pool_h, self.pool_w, self.stride, self.pad)
        col = col.reshape(-1, self.pool_h * self.pool_w)

        arg_max = np.argmax(col, axis=1)
        out = np.max(col, axis=1)
        out = out.reshape(N, out_h, out_w, C).transpose(0, 3, 1, 2)

        self.x = x
        self.arg_max = arg_max

        return out

    def backward(self, dout):
        dout = dout.transpose(0, 2, 3, 1)

        pool_size = self.pool_h * self.pool_w
        dmax = np.zeros((dout.size, pool_size))
        dmax[np.arange(self.arg_max.size), self.arg_max.flatten()] = dout.flatten()
        dmax = dmax.reshape(dout.shape + (pool_size,))

        dcol = dmax.reshape(dmax.shape[0] * dmax.shape[1] * dmax.shape[2], -1)
        dx = col2im(dcol, self.x.shape, self.pool_h, self.pool_w, self.stride, self.pad)

        return dx


# 更新梯度方法
## SGD随机梯度下降方法(最常用)
class SGD:
    def __init__(self, lr=0.01):
        self.lr = lr

    def update(self, params, grads):
        for key in params.keys():
            params[key] -= self.lr * grads[key]


## Momentum动量方法
class Momentum:
    def __init__(self, lr=0.01, momentum=0.9):
        self.lr = lr
        self.momentum = momentum
        self.v = None

    def update(self, params, grads):
        if self.v is None:
            self.v = {}  # 速度也是每一个参数对应一个速度
            for key, val in params.items():
                self.v[key] = np.zeros_like(val)
        for key in params.keys():
            self.v[key] = self.momentum * self.v[key] - self.lr * grads[key]  # αv-lr*grads
            params[key] += self.v[key]


## AdaGrad方法
class AdaGrad:
    def __init__(self, lr=0.01):
        self.lr = lr
        self.h = None

    def update(self, params, grads):
        if self.h is None:
            self.h = {}
            for key, val in params.items():
                self.h[key] = np.zeros_like(val)
        for key in params.keys():
            self.h[key] += grads[key] * grads[key]
            params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)  # 就是照着书上那个公式来实现


# 一些神经网络类
## 2层神经网络(数值微分)
class TwoLayerNet_Numerical:
    def __init__(self, input_size, hidden_size, output_size,
                 weight_init_std=0.01):  # weight_init_std是权重初始值随机高斯分布的标准差 因为需要让权重尽量小
        self.params = {}  # 权重参数字典
        self.params['w1'] = weight_init_std * np.random.randn(input_size, hidden_size)  # 权重 初始化为较小的高斯分布
        self.params['b1'] = np.zeros(hidden_size)  # 偏置 初始化为0
        self.params['w2'] = weight_init_std * np.random.randn(hidden_size, output_size)
        self.params['b2'] = np.zeros(output_size)

    def predict(self, x):
        w1, w2 = self.params['w1'], self.params['w2']
        b1, b2 = self.params['b1'], self.params['b2']
        a1 = np.dot(x, w1) + b1
        z1 = sigmoid(a1)  # 第一层结束
        a2 = np.dot(z1, w2) + b2
        y = sigmoid(a2)  # 第二层结束
        return y

    def loss(self, x, t):  # 求算代价
        y = self.predict(x)
        return cross_entropy_error(y, t)

    def accuracy(self, x, t):  # 求算网络准确值
        y = self.predict(x)
        y = np.argmax(y, axis=1)
        t = np.argmax(t, axis=1)
        accuracy = np.sum(y == t) / float(y.shape[0])
        return accuracy

    def numerical_gradient(self, x, t):
        loss_w = lambda w: self.loss(x, t)
        grads = {}
        grads['w1'] = numerical_gradient(loss_w, self.params['w1'])
        grads['w2'] = numerical_gradient(loss_w, self.params['w2'])
        grads['b1'] = numerical_gradient(loss_w, self.params['b1'])
        grads['b2'] = numerical_gradient(loss_w, self.params['b2'])
        return grads


## 2层神经网络(反向传播)
class TwoLayerNet_BackPropagation:
    def __init__(self, input_size, hidden_size, output_size,
                 weight_init_std=0.01):  # weight_init_std是权重初始值随机高斯分布的标准差 因为需要让权重尽量小
        self.params = {}  # 权重参数字典
        self.params['w1'] = np.random.randn(input_size, hidden_size) / np.sqrt(input_size)  # 权重 初始化方法是Xavier高斯分布
        self.params['b1'] = np.zeros(hidden_size)  # 偏置 初始化为0
        self.params['w2'] = np.random.randn(hidden_size, output_size) / np.sqrt(hidden_size)
        self.params['b2'] = np.zeros(output_size)
        # 生成层
        self.layers = OrderedDict()  # 注意是有序字典  而且这里存放的是除了最后一层以外的所有层  最后一层有特殊用处
        self.layers['Affine1'] = Affine(self.params['w1'], self.params['b1'])
        self.layers['Relu1'] = Relu()
        self.layers['Affine2'] = Affine(self.params['w2'], self.params['b2'])
        self.lastlayer = SoftmaxWithLoss();

    def predict(self, x):
        for layer in self.layers.values():  # 注意这里的语法.values()
            x = layer.forward(x)
        return x

    def loss(self, x, t):  # 求算代价
        y = self.predict(x)
        return self.lastlayer.forward(y, t)

    def accuracy(self, x, t):  # 求算网络准确值
        y = self.predict(x)
        y = np.argmax(y, axis=1)
        if t.ndim != 1: t = np.argmax(t, axis=1)
        accuracy = np.sum(y == t) / float(y.shape[0])
        return accuracy

    def gradient(self, x, t):
        self.loss(x, t)
        # 反向传播
        dout = 1
        dout = self.lastlayer.backward(dout)

        layers = list(self.layers.values())
        layers.reverse()  # 顺序倒置  目的就是反向传播
        for layer in layers:
            dout = layer.backward(dout)
        grads = {}
        grads['w1'] = self.layers['Affine1'].dw
        grads['w2'] = self.layers['Affine2'].dw
        grads['b1'] = self.layers['Affine1'].db
        grads['b2'] = self.layers['Affine2'].db
        return grads

    def numerical_gradient(self, x, t):  # 这个数值微分法还是要留着 为了梯度验证
        loss_w = lambda w: self.loss(x, t)
        grads = {}
        grads['w1'] = numerical_gradient(loss_w, self.params['w1'])
        grads['w2'] = numerical_gradient(loss_w, self.params['w2'])
        grads['b1'] = numerical_gradient(loss_w, self.params['b1'])
        grads['b2'] = numerical_gradient(loss_w, self.params['b2'])
        return grads

    def gradient_check(self, x, t):
        x_check = x[:5]
        t_check = t[:5]
        grad_numerical = self.numerical_gradient(x_check, t_check)
        grad_backprop = self.gradient(x_check, t_check)
        # 求平均值
        for key in grad_backprop.keys():
            diff = np.average(np.abs(grad_numerical[key] - grad_backprop[key]))
            print(key + ":" + str(diff))
        return


## 多层神经网络(书中提供的实现)
class MultiLayerNet:
    def __init__(self, input_size, hidden_size_list, output_size,
                 activation='relu', weight_init_std='relu', weight_decay_lambda=0):
        self.input_size = input_size
        self.output_size = output_size
        self.hidden_size_list = hidden_size_list
        self.hidden_layer_num = len(hidden_size_list)
        self.weight_decay_lambda = weight_decay_lambda
        self.params = {}

        # 初始化权重
        self.__init_weight(weight_init_std)

        # 生成层
        activation_layer = {'sigmoid': Sigmoid, 'relu': Relu}
        self.layers = OrderedDict()
        for idx in range(1, self.hidden_layer_num + 1):
            self.layers['Affine' + str(idx)] = Affine(self.params['W' + str(idx)],
                                                      self.params['b' + str(idx)])
            self.layers['Activation_function' + str(idx)] = activation_layer[activation]()

        idx = self.hidden_layer_num + 1
        self.layers['Affine' + str(idx)] = Affine(self.params['W' + str(idx)],
                                                  self.params['b' + str(idx)])

        self.last_layer = SoftmaxWithLoss()

    def __init_weight(self, weight_init_std):  # 设定权重的初始值   可以用Sigmoid或者ReLU
        all_size_list = [self.input_size] + self.hidden_size_list + [self.output_size]
        for idx in range(1, len(all_size_list)):
            scale = weight_init_std
            if str(weight_init_std).lower() in ('relu', 'he'):
                scale = np.sqrt(2.0 / all_size_list[idx - 1])  # 使用ReLU的情况下推荐的初始值
            elif str(weight_init_std).lower() in ('sigmoid', 'xavier'):
                scale = np.sqrt(1.0 / all_size_list[idx - 1])  # 使用sigmoid的情况下推荐的初始值

            self.params['W' + str(idx)] = scale * np.random.randn(all_size_list[idx - 1], all_size_list[idx])
            self.params['b' + str(idx)] = np.zeros(all_size_list[idx])

    def predict(self, x):
        for layer in self.layers.values():
            x = layer.forward(x)
        return x

    def loss(self, x, t):
        y = self.predict(x)
        weight_decay = 0
        for idx in range(1, self.hidden_layer_num + 2):
            W = self.params['W' + str(idx)]
            weight_decay += 0.5 * self.weight_decay_lambda * np.sum(W ** 2)
        return self.last_layer.forward(y, t)
        # return self.last_layer.forward(y, t) + weight_decay  # 后面加上weight_decay是权值参数正则化

    def accuracy(self, x, t):
        y = self.predict(x)
        y = np.argmax(y, axis=1)
        if t.ndim != 1: t = np.argmax(t, axis=1)

        accuracy = np.sum(y == t) / float(x.shape[0])
        return accuracy

    def numerical_gradient(self, x, t):
        loss_W = lambda W: self.loss(x, t)
        grads = {}
        for idx in range(1, self.hidden_layer_num + 2):
            grads['W' + str(idx)] = numerical_gradient(loss_W, self.params['W' + str(idx)])
            grads['b' + str(idx)] = numerical_gradient(loss_W, self.params['b' + str(idx)])

        return grads

    def gradient(self, x, t):
        # forward
        self.loss(x, t)
        # backward
        dout = 1
        dout = self.last_layer.backward(dout)
        layers = list(self.layers.values())
        layers.reverse()
        for layer in layers:
            dout = layer.backward(dout)
        grads = {}
        for idx in range(1, self.hidden_layer_num + 2):
            grads['W' + str(idx)] = self.layers['Affine' + str(idx)].dw + self.weight_decay_lambda * self.layers[
                'Affine' + str(idx)].w
            grads['b' + str(idx)] = self.layers['Affine' + str(idx)].db
        return grads


# 进行神经网络训练的类(书中提供的代码 目前暂时没用 以后可以拿过来扩展一下)
class Trainer:
    def __init__(self, network, x_train, t_train, x_test, t_test,
                 epochs=20, mini_batch_size=100,
                 optimizer='SGD', optimizer_param={'lr': 0.01},
                 evaluate_sample_num_per_epoch=None, verbose=True):
        self.network = network
        self.verbose = verbose
        self.x_train = x_train
        self.t_train = t_train
        self.x_test = x_test
        self.t_test = t_test
        self.epochs = epochs
        self.batch_size = mini_batch_size
        self.evaluate_sample_num_per_epoch = evaluate_sample_num_per_epoch

        # optimzer
        optimizer_class_dict = {'sgd': SGD, 'momentum': Momentum, 'adagrad': AdaGrad}
        self.optimizer = optimizer_class_dict[optimizer.lower()](**optimizer_param)

        self.train_size = x_train.shape[0]
        self.iter_per_epoch = max(self.train_size / mini_batch_size, 1)
        self.max_iter = int(epochs * self.iter_per_epoch)
        self.current_iter = 0
        self.current_epoch = 0

        self.train_loss_list = []
        self.train_acc_list = []
        self.test_acc_list = []

    def train_step(self):
        batch_mask = np.random.choice(self.train_size, self.batch_size)
        x_batch = self.x_train[batch_mask]
        t_batch = self.t_train[batch_mask]

        grads = self.network.gradient(x_batch, t_batch)
        self.optimizer.update(self.network.params, grads)

        loss = self.network.loss(x_batch, t_batch)
        self.train_loss_list.append(loss)
        if self.verbose: print("train loss:" + str(loss))

        if self.current_iter % self.iter_per_epoch == 0:
            self.current_epoch += 1

            x_train_sample, t_train_sample = self.x_train, self.t_train
            x_test_sample, t_test_sample = self.x_test, self.t_test
            if not self.evaluate_sample_num_per_epoch is None:
                t = self.evaluate_sample_num_per_epoch
                x_train_sample, t_train_sample = self.x_train[:t], self.t_train[:t]
                x_test_sample, t_test_sample = self.x_test[:t], self.t_test[:t]

            train_acc = self.network.accuracy(x_train_sample, t_train_sample)
            test_acc = self.network.accuracy(x_test_sample, t_test_sample)
            self.train_acc_list.append(train_acc)
            self.test_acc_list.append(test_acc)

            if self.verbose: print(
                "=== epoch:" + str(self.current_epoch) + ", train acc:" + str(train_acc) + ", test acc:" + str(
                    test_acc) + " ===")
        self.current_iter += 1

    def train(self):
        for i in range(self.max_iter):
            self.train_step()

        test_acc = self.network.accuracy(self.x_test, self.t_test)

        if self.verbose:
            print("=============== Final Test Accuracy ===============")
            print("test acc:" + str(test_acc))


# 主函数main()部分 用类实现 以便多个神经网络不冲突在一块儿
class Main:
    def tryTwoLayerNet_Numerical(self):
        """
            一个简单的二层神经网络
            其中激活函数采用sigmoid  初始化权重采用普通SGD  代价函数采用交叉熵误差
            未采用模块化神经层
            **求梯度采用数值微分**  下降时采用固定学习率
            使用mini-batch优化
            运行情况:

        """
        start_time = time.time()
        (x_train, t_train), (x_test, t_test) = load_mnist(one_hot_label=True, normalize=True)  # 获取mnist
        train_loss_list = []  # 训练代价函数变化情况记录在列表里
        # 超参数部分
        learn_time = 2  # 梯度下降法次数   这个算法巨慢!! 扩大学习次数要慎重
        train_size = x_train.shape[0]
        batch_size = 100
        learning_rate = 0.1  # 梯度下降法学习率
        network = TwoLayerNet_Numerical(input_size=784, hidden_size=50, output_size=10)

        for i in range(learn_time):  # 更新下降iters_num次
            print(i)
            # 获取mini-batch
            batch_mask = np.random.choice(train_size, batch_size)
            x_batch = x_train[batch_mask]
            t_batch = t_train[batch_mask]
            # 计算grads 更新参数
            grads = network.numerical_gradient(x_batch, t_batch)
            for key in ('w1', 'b1', 'w2', 'b2'):
                network.params[key] -= learning_rate * grads[key]
            loss = network.loss(x_batch, t_batch)
            train_loss_list.append(loss)

        x = range(learn_time)
        plt.plot(x, train_loss_list)
        end_time = time.time()
        run_time = end_time - start_time
        print("本次运行时间:%.2f秒" % run_time)
        print("平均一次学习时长:%.2f秒" % (run_time / learn_time))

        plt.show()
        return

    def tryTwoLayerNet_BackPropagation(self):
        """
            一个简单的二层神经网络
            其中激活函数采用Softmax 初始化权重为Xavier高斯分布  代价函数采用交叉熵误差
            采用模块化神经层
            **求梯度采用反向传播**  下降时采用SGD下降法
            使用mini-batch优化
        """
        start_time = time.time()
        (x_train, t_train), (x_test, t_test) = load_mnist(one_hot_label=True, normalize=True)  # 获取mnist
        train_loss_list = []  # 训练代价函数变化情况记录在列表里
        train_accuracy_list = []
        test_accuracy_list = []  # 训练集和验证集的准确率记录在列表里
        # 超参数部分
        learn_time = 50000  # 梯度下降法次数
        train_size = x_train.shape[0]
        batch_size = 10
        learning_rate = 0.1  # 梯度下降法学习率
        network = TwoLayerNet_BackPropagation(input_size=784, hidden_size=50, output_size=10)
        oneepoch_time = max(train_size // batch_size, 1)

        ### network.gradient_check(x_train,t_train)     # 梯度验证

        for i in range(learn_time):  # 更新下降learn_time次
            print(i)
            # 获取mini-batch
            batch_mask = np.random.choice(train_size, batch_size)
            x_batch = x_train[batch_mask]
            t_batch = t_train[batch_mask]
            # 计算grads 更新参数
            grads = network.gradient(x_batch, t_batch)  # 鸟枪换炮
            """
            for key in ('w1', 'b1', 'w2', 'b2'):
                network.params[key] -= learning_rate * grads[key]
            """
            # SGD下降法
            SGD().update(network.params, grads)
            loss = network.loss(x_batch, t_batch)
            train_loss_list.append(loss)
            if (i % oneepoch_time == 0):  # 差不多循环完一次数据集了 来记录一下准确率
                train_acc = network.accuracy(x_train, t_train)
                test_acc = network.accuracy(x_test, t_test)
                train_accuracy_list.append(train_acc)
                test_accuracy_list.append(test_acc)

        x1 = range(learn_time)
        plt.subplot(1, 2, 1)
        plt.plot(x1, train_loss_list)  # 第一个图像展示代价函数
        x2 = range(train_accuracy_list.__len__())
        plt.subplot(1, 2, 2)
        plt.plot(x2, train_accuracy_list, label="train")  # 第二个函数展示精确度
        plt.plot(x2, test_accuracy_list, label="test")
        end_time = time.time()
        run_time = end_time - start_time
        print("本次运行时间:%.2f秒" % run_time)
        print("平均一次学习时长:%.2f秒" % (run_time / learn_time))

        plt.show()
        return

    def tryMultyLayerNet(self):
        """
            全连接的多层神经网络  主要是书中提供的实现
            Parameters
            ----------
            input_size : 输入大小（MNIST的情况下为784）
            hidden_size_list : 隐藏层的神经元数量的列表（e.g. [100, 100, 100]）
            output_size : 输出大小（MNIST的情况下为10）
            activation : 'relu' or 'sigmoid'
            weight_init_std : 指定权重的标准差（e.g. 0.01）
                指定'relu'或'he'的情况下设定“He的初始值”
                指定'sigmoid'或'xavier'的情况下设定“Xavier的初始值”
            weight_decay_lambda : Weight Decay（L2范数）的强度


        """
        start_time = time.time()
        (x_train, t_train), (x_test, t_test) = load_mnist(one_hot_label=True, normalize=True)  # 获取mnist
        train_loss_list = []  # 训练代价函数变化情况记录在列表里
        train_accuracy_list = []
        test_accuracy_list = []  # 训练集和验证集的准确率记录在列表里
        # 超参数部分
        learn_time = 50000  # 梯度下降法次数
        train_size = x_train.shape[0]
        batch_size = 100
        learning_rate = 0.1  # 梯度下降法学习率
        network = MultiLayerNet(input_size=784, hidden_size_list=[50 for i in range(4)], output_size=10)
                                        # 这里面的hidden_size_list 就可以设置隐藏层每一层的神经元个数以及隐藏层层数
        oneepoch_time = max(train_size // batch_size, 1)

        ### network.gradient_check(x_train,t_train)     # 梯度验证
        train_acc = test_acc = None
        for i in range(learn_time):  # 更新下降learn_time次
            print(i)
            # 获取mini-batch
            batch_mask = np.random.choice(train_size, batch_size)
            x_batch = x_train[batch_mask]
            t_batch = t_train[batch_mask]
            # 计算grads 更新参数
            grads = network.gradient(x_batch, t_batch)  # 鸟枪换炮
            """
            for key in ('w1', 'b1', 'w2', 'b2'):
                network.params[key] -= learning_rate * grads[key]
            """
            # SGD下降法
            SGD().update(network.params, grads)
            loss = network.loss(x_batch, t_batch)
            train_loss_list.append(loss)
            if (i % oneepoch_time == 0):  # 差不多循环完一次数据集了 来记录一下准确率
                train_acc = network.accuracy(x_train, t_train)
                test_acc = network.accuracy(x_test, t_test)
                train_accuracy_list.append(train_acc)
                test_accuracy_list.append(test_acc)

        x1 = range(learn_time)
        plt.subplot(1, 2, 1)
        plt.plot(x1, train_loss_list)  # 第一个图像展示代价函数
        x2 = range(train_accuracy_list.__len__())
        plt.subplot(1, 2, 2)
        title_str = str(network.hidden_layer_num + 1) + "-Layers-Net LearningMap"
        plt.title(title_str)
        plt.plot(x2, train_accuracy_list, label="train")  # 第二个函数展示精确度
        plt.plot(x2, test_accuracy_list, label="test")
        end_time = time.time()
        run_time = end_time - start_time
        print("本次运行为{}层网络 学习{}次 耗时:{:.2f}秒".format(network.hidden_layer_num + 1, learn_time, run_time))
        print("训练集准确率为{:.2f}% 验证集准确率为{:.2f}%".format((train_acc * 100.0), (test_acc * 100.0)))
        plt.legend()
        plt.show()
        return


# main()主函数部分
Main().tryMultyLayerNet()