What is FFT? FFT学习笔记

在时间序列、数字信号的数据处理中经常会看到使用FFT作为一段数据中提取频率的手段，但是往往文中没有花大笔墨去解释，仿佛所有人都了解这个概念。

FFT(Fast Fourier Transform) 为快速傅里叶变换，是一种高效计算DFT(Discrete Fourier Transform)，离散傅里叶变换的方法。在了解FFT之前需要先了解DFT的作用。

DFT

离散傅里叶变换（Discrete Fourier Transform，简称DFT）是一种数学算法，用于将一个序列或信号从时域转换到频域，广泛应用于信号处理、图像处理、音频分析、通信系统等领域。时域是指信号随时间的变化，而频域则描述了信号中不同频率成分的分布。人话说，就是由一段x=时间; y=幅度 的信号数据转换成为x=频率 ; y=幅度 的数据，可以参考以下这个图：

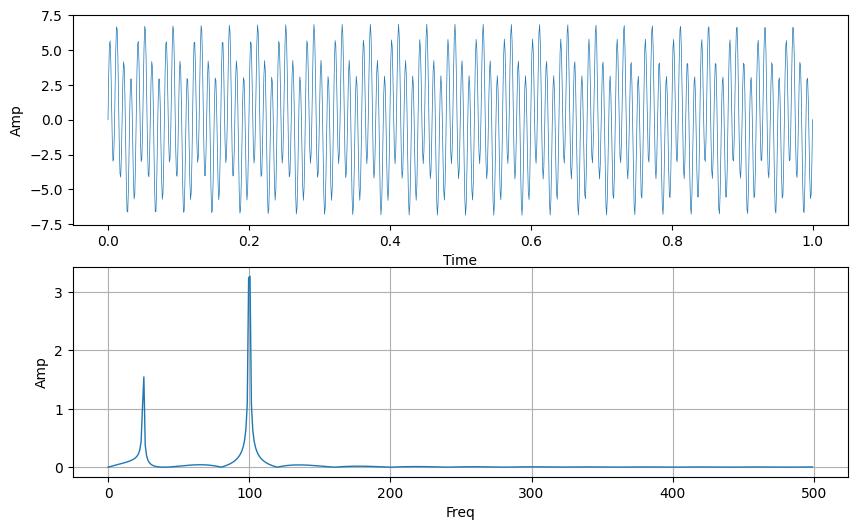
原信号（上图）中存在两种不同的频率（f=25 和 f=100），通过DFT提取可以看到下图中，它们在频域上显示了两个峰出来。在频域中，信号被表示为一系列频率成分，每个成分由一个幅度(amplitude)和相位(phase)组成。

DFT是傅里叶分析在离散信号处理领域的核心工具，主要目的是将离散信号（时域信号）转换成其对应的频。与连续信号不同，离散信号在时间上是分隔的，例如数字音频或图像数据。

数学表达

DFT将一个长度为\(n\)的复数或实数序列 \( [x_0, x1, …, x{n-1}]\) 转换成另一个长度为 \(n\) 的复数序列 \([X_0, X1, …, X{n-1}]\) 转换的公式为

\[X(k) = \sum_{j=0}^{n-1} \mathbf{x}_n \cdot e^{-i \frac{2\pi}{n}kj} \tag{1} \label{eq1} \]

其中，\(i\) 是虚数单位，\(k\)是当前频率的索引。

由于因为它涉及对每个输出频率 \(X_k\) 进行 \(n\) 次复数乘法和加法操作，直接计算的复杂度为 \(O(n^2)\)，因此往往都会使用FFT来进行高效计算。FFT并不改变DFT的结果，只是提供了一种更快的计算方式。

FFT

FFT主要采用了一些技巧来简化流程。

复数单位根

首先将以上公式\(\eqref{eq1}\)中的指数部分写为以下格式：

\[e^{-i\frac{2\pi}{n} kj}=\omega_n^{kj}, \text{where }\omega_n =e^{-i\frac{2\pi}{n}} \]

证明：

Definition: 如果一个复数\(\omega ^n=1\), 我们将\(\{\omega_n^k\}, k=1,…n\) 定义为n次单位根。n次单位根有三个性质，后面会用到：

\[\text{1. }\omega^kn = \omega^{2k}{2n} \quad \text{2. }\omega^kn = -\omega^{k+\frac{n}{2}}{n}\quad \text{3. }\omega^0n = \omega^{n}{n}=1 \tag{2}\label{eq2} \]

由于欧拉公式 \(e^{\pi i}=-1\)，我们可以得出 \(\omega_n :=e^{-i\frac{2\pi}{n}}\) 是一个n次单位根。再做一些简单的幂运算就可以得出上面的公式

多项式变换

首先确定几个notation，我们要处理的信号数据是 \(\mathbf{x} \in \mathbb{R}^T\)（暂时假设是一维），是一个长度为\(T\)的数组。\(\mathbf{x}_n\) 代表了在n时间点上信号数据的值。

我们使用\(f(x)\)来指代需要进行的FFT计算，注意这里 \(x\) 和 \(\mathbf{x}\) 不同。将公式\(\eqref{eq1}\)的多项式可以展开为一个多项式t

\[f(x) = \mathbf{x}_0 + \mathbf{x}_1x + \mathbf{x}_2x^2+\mathbf{x}3x^3+…+\mathbf{x}{n-1}x^{n-1} \]

让我们不失一般性地，假设\(n=2^s\)，因为我们可以将一个多项式延展到更高次的多项式，将系数设为0。让我们根据\(\mathbf{x}_n\)下标的奇偶性将\(f(x)\)分为两个部分：

\[\begin{aligned} f(x) & = (\mathbf{x}_0 + \mathbf{x}_2x^2+\mathbf{x}4x^4+…+\mathbf{x}{n-2}x^{n}) + (\mathbf{x}_1x+\mathbf{x}_3x^3+\mathbf{x}5x^5+…+\mathbf{x}{n-1}x^{n-1}) \\ & = (\mathbf{x}_0 + \mathbf{x}_2x^2+\mathbf{x}4x^4+…+\mathbf{x}{n-2}x^{n})+x \cdot (\mathbf{x}_1 + \mathbf{x}_3x^2+\mathbf{x}5x^4+…+\mathbf{x}{n-1}x^{n-1}) \\ & = f_1(x^2)+xf_2(x^2)\\ \text{where:}&\\ f_1(x) & = \mathbf{x}_0 + \mathbf{x}_2x^2+\mathbf{x}4x^4+…+\mathbf{x}{n-2}x^{n}\\ f_2(x) & = \mathbf{x}_1x+\mathbf{x}_3x+\mathbf{x}5x^4+…+\mathbf{x}{n-1}x^{n-1} \end{aligned} \]

将公式 \(\eqref{eq1}\) 中的 \(\omega_n^k =e^{-i\frac{2\pi}{n}k}\) 作为 \(x\) 带入，根据单位根性质 \(\eqref{eq2}\) 中的 \(\omega^kn = \omega^{2k}{2n}\) 可得：

\[\begin{aligned} f(\omega_n^k) &= f_1(\omega_n^{2k})+\omega_n^{k}\cdot f_2(\omega_n^{2k}) \\ \omega^kn = \omega^{2k}{2n} &\Rightarrow \\ &= f1(\omega{\frac{n}{2}}^k) + \omega_n^{k}\cdot f2(\omega{\frac{n}{2}}^k) \\ \end{aligned} \]

将\(x=\omega_n^{k+\frac{n}{2}}\) 带入，再根据单位根性质可得

\[\begin{aligned} f(\omega_n^{k+\frac{n}{2}}) &= f_1(\omega_n^{2k+n})+\omega_n^{k+\frac{n}{2}} \cdot f_2(\omega_n^{2k+n})\
\omega^kn = -\omega^{k+\frac{n}{2}}{n}, \omega^0n = \omega^{n}{n}=1 &\Rightarrow \\ &= f_1(\omega_n^{2k}) - \omega_n^k f_2(\omega_n^{2k}) \\ &= f1(\omega\frac{n}{2}^{k}) - \omega_n^k f2(\omega\frac{n}{2}^{k}) \end{aligned} \]

因此，通过计算 \(f1(\omega\frac{n}{2}^{k}), \omega_n^k f2(\omega\frac{n}{2}^{k})\) 可以通过 \(\text{O(logn)}\) 复杂度计算得到 \(f(\omega_n^k), f(\omega_n^{k+\frac{n}{2}})\) ，再通过 \(\text{O(nlogn)}\) 计算得到多项式所有的项。