论文标题：Causal Intervention and Counterfactual Reasoning for Multi-modal Fake News Detection
论文作者：Ziwei Chen, Linmei Hu, Weixin Li, Yingxia Shao, Liqiang Nie
论文来源：ACL 2023，Paper
代码来源：未公布

---

目录

• 引入
  • 贡献
• 基本知识介绍
  • 因果图
  • 因果关系的干预
  • 反事实推理与因果效应
• 方法
  • 虚假新闻检测的因果图
  • 用因果干预进行去混淆训练
  • 用反事实推理减轻图像偏见
  • 训练与推理

引入

为了明确地解释数据偏差 ，我们首先将假新闻检测的过程表述为如图(a)所示的因果图 。
除了多模态假新闻检测方法关注的融合特征\(C\)对新闻标签\(Y\)的影响外，另外两条边分别从文本特征\(T\)和图像特征\(I\)出发，指向\(Y\)。

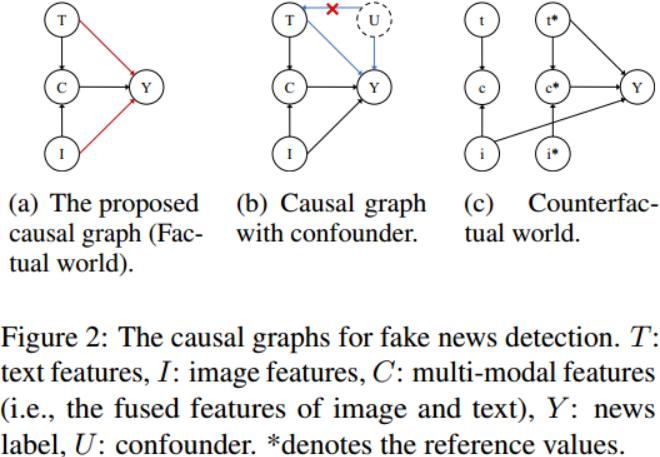
一般来说，假新闻的发布者会尽力编造令人困惑的文字，或者使用一定的技术伪造假图像。这使得文本和图像可以单独影响新闻标签 。

\(T \rightarrow Y\)：文本的语言特征具有明显的情感偏好 。

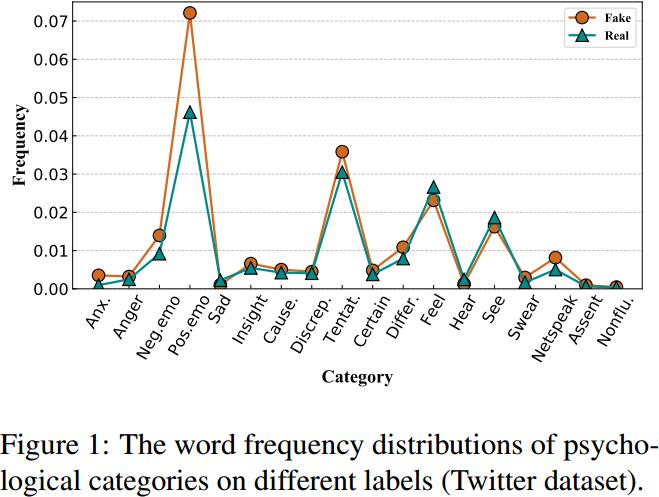
图中不难看出：假新闻更喜欢使用负面情绪的语言词 来激起读者的情绪。这使得模型可能容易依赖这些表达心理情绪的语言特征 作为判断新闻真实性的捷径。但对训练集和测试集进行分析发现这些心理语言词汇的出现频率存在显著差异，证明了这种捷径似乎是不可靠的证据。如图(b)所示，其中\(U\)表示混杂因素(即文本中的心理语言特征)，存在一条后门路径\(T←U→Y\)，该路径将引入文本特征和新闻标签之间的虚假相关性。
为了消除心理语言偏差 ，采用后门调整 来计算训练阶段的因果效应。

\(I \rightarrow Y\)：共享同一图像的两个不同的新闻片段可能具有相反的标签 。
这表明，有时即使图像是真实的，文字也可能是捏造的 。虽然可以利用图像作为一种额外的方式来提供更多的检测证据，但是仅仅根据图像特征 来推断新闻的真实性是不可靠的。所以有必要消除图像偏见 。
可以使用反事实推理，通过想象一个反事实的世界（图©），其中，除了图像特征\(I\)，文本特征\(T\)和融合特征\(C\)都没有给出(由参考值\(t^∗\)和\(c^∗\)表示),如此，可以通过计算\(I\)对\(Y\)的直接因果效应来估计偏差，我们可以通过从对\(Y\)的总影响中减去它来进行消除偏差。

贡献

• 分析了假新闻检测数据的每种模式，并确定了文本和图像偏见中潜在的心理语言偏见，在此基础上，提出了一种基于因果干预和反事实推理的多模态假新闻脱偏框架(CCD)；
• 为了解决图像偏见，我们采用反事实推理来追求间接因果效应作为推理预测；
• 因果框架CCD可以应用于任何以图像和文本特征作为输入的假新闻检测模型。我们在三个强基线模型上实施了所提出的框架，并在两个广泛使用的基准数据集上进行了大量实验，验证了CCD的有效性。

---

基本知识介绍

因果图

一种概率图模型，用于描述变量之间如何相互作用，由变量集\(\mathcal{N}\)和两个节点之间的因果关系\(\mathcal E\)组成的有向无环图\(G = \{ \mathcal N, \mathcal E \}\)表示。如图所示，\(X→Y\)表示\(X\)是\(Y\)的原因，\(U\)是混杂因素。

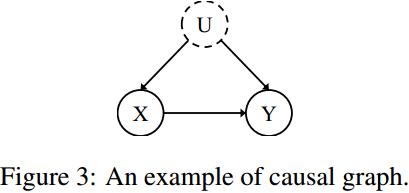
因果关系的干预

因果干预是在存在混杂因素的情况下，寻求一个变量对另一个变量的真实因果关系。在因果图中，对变量的干预操作会删除指向它的所有边，这样它的父节点就不再导致它。

带do- calculus的后门调整提供了一种在没有额外混杂因素的情况下计算干预分布的工具。以上图为例，根据贝叶斯定理可推导出调整公式如下，其中\(u\)表示混动因子\(U\)的值：

\[P(Y \mid d o(X))=\sum_{u} P(Y \mid X, u) P(u) \tag{1} \]

反事实推理与因果效应

反事实推理是一种统计推理方法，用于推断与事实世界不同的假设条件下的结果。下图显示了一个用于估计和消除\(X\)对\(Y\)的直接影响的抽象设置。

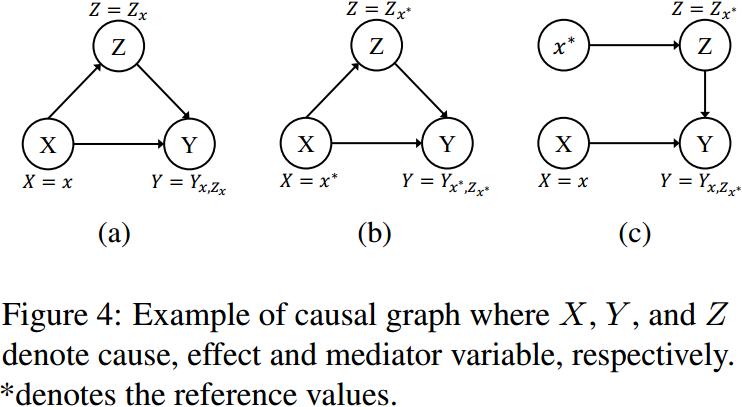
图(a)是实际世界，其中\(Y\)的计算为\(Y{x, Z{x}}=Y(X=x, Z=Z(X=x))\)

基于图(a)和图(b)，将\(X=x\)对\(Y\)的总效应(TE)定义为：

\[\mathrm{TE}=Y{x, Z{x}}-Y{x^{*}, Z{x^{*}}} \tag{2} \]

这可以看作是X在两种不同处理下的两种潜在结果的比较，即\(X=x\)和\(X=x^{*}\)
总效应(TE)可以分解为自然直接效应(NDE)和总间接效应(TIE)之和，即TE = NDE + TIE。
当中介变量\(Z\)被阻断时，NDE表示\(X\)对\(Y\)的自然直接影响（图©）：

\[\mathrm{NDE}=Y{x, Z{x^{}}}-Y_{x^{}, Z_{x^{*}}} \tag{3} \]

\(Y{x, Z{x^{*}}}\)是在反事实世界下计算的，其中\(X\)可以同时设为不同的值\(x\)和\(x^∗\)（图©）。因此可以得到TIE (\(X\)对\(Y\)的总间接效应)：

\[\mathrm{TIE}=\mathrm{TE}-\mathrm{NDE}=Y{x, Z{x}}-Y{x, Z{x^{*}}} \tag{4} \]

我们使用TIE作为去偏结果进行推理。

---

方法

在本节中，首先将假新闻检测任务制定为因果图 ，以清楚地描述因素之间的因果关系。然后，提出了CCD框架，通过因果干预 来消除心理语言偏见 ，并通过反事实推理 推导出图像特征的直接因果效应(即图像偏见)

虚假新闻检测的因果图

因果图如图(a)所示，其中每个分支都可以通过一个基本的假新闻检测模型来实现。该模型的抽象格式应为：

\[Y_{t, i, c}=Y(T=t, I=i, C=c) \tag{5} \]

其中，\(c=f(T=t, I=i)\)，\(f(·)\)为基线假新闻检测模型中的特征聚合函数。

那么对标签\(y\)的总影响(TE)可以写成：

\[\mathrm{TE}=Y{t, i, c}-Y{t^{}, i^{}, c^{*}} \tag{6} \]

如之前所述，“*”状态被定义为阻断来自文本和图像的信号的状态，即\(t\)和\(i\)不给定(void值)。为了方便实现，使用用标量值0填充的张量来表示参考值\(t^∗\)和\(i^∗\)。这样，输入就不包含任何语义信息。

通过具有融合函数的模型集成计算预测值：

\[\begin{aligned} Y{t, i, c} & =Y(T=t, I=i, C=c) \\ & =\mathcal{F}\left(Y{t}, Y{i}, Y{c}\right) \\ & =Y{c}+\tanh \left(Y{t}\right)+\tanh \left(Y_{i}\right) \end{aligned} \tag{7} \]

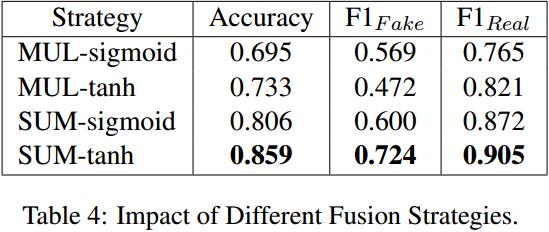
其中，\(\mathcal{F}(·)\)是得到最终预测的融合函数。采用非线性融合策略以获得更好的表示能力，任何可微算术二进制运算都可以用作融合函数\(\mathcal{F}(·)\)，下表给出了不同融合函数的影响。

用因果干预进行去混淆训练

如图(b)所示，存在一个未观察到的混杂因素\(U\)(即文本的心理语言词)，它通过学习似然\(P(Y|T)\)导致文本特征与新闻标签之间的虚假关联。
为了明确说明混淆因素的影响，我们使用贝叶斯定理：

\[\begin{aligned} P(Y \mid T) & =\sum{u} P(Y \mid T, u) P(u \mid T) \\ & \propto \sum{u} P(Y \mid T, u) P(T \mid u) P(u) \end{aligned} \tag{8} \]

接下来，在\(T→Y\)分支进行去混淆训练，利用后门调整对\(T\)进行do-calculus，计算出相应的干预分布。
由于边缘\(U→T\)已经被截断，我们可以得到：

\[\begin{aligned} Y{t} & =P(Y \mid d o(T)) \\ & =\sum{u} P(Y \mid T, u) P(u) \end{aligned} \tag{9} \]

要估算\(Y{t}\)，给定文本特征表示\(t\)和混淆表示\(u\)，公式(9)可以变为\(\sum{\mathbf{u}} P(y \mid \mathbf{t}, \mathbf{u}) P(\mathbf{u})\)，其中\(P(y \mid \mathbf{t}, \mathbf{u})\)是一个新闻特征学习模型\(g(·)\)的预测输出：

\[P(y \mid \mathbf{t}, \mathbf{u})=\sigma(g(\mathbf{t}, \mathbf{u})) \tag{10} \]

其中\(\sigma(·)\)是sigmoid函数。

综上，公式(9)的实现可以正式定义为：

\[\begin{aligned} P(Y \mid d o(T)) & =\mathbb{E}{u}[P(Y \mid T, u)] \\ & =\mathbb{E}{u}[\sigma(g(\mathbf{t}, \mathbf{u}))] \end{aligned} \tag{11} \]

由于直接计算\(\mathbb{E}_{u}\)需要非常多的采样，可以应用归一化加权几何平均(NWGM)通过将外部期望移动到sigmo函数中来近似上述期望：

\[P(Y \mid d o(T)) \stackrel{\text { NWGM }}{\approx} \sigma\left(\mathbb{E}_{u}[g(\mathbf{t}, \mathbf{u})]\right) \tag{12} \]

我们采用线性模型来近似条件概率，即\(Y\)在条件\(T\)和\(U\)下的概率。我们建立模型\(g(\mathbf{t}, \mathbf{u})=\mathbf{W}{t} \mathbf{t}+\mathbf{W}{u} \cdot h(\mathbf{u})\)，其中\(h(\mathbf{u})\)是\(\mathbf{u}\)的特征变换，\(\mathbf{W}{t}\)和\(\mathbf{W}{u}\)为可学习的权重参数。在这样的情况下，\(\mathbb{E}{u}[g(\mathbf{t}, \mathbf{u})] = \mathbf{W}{t} \mathbf{t} + \mathbb{E}_{u}[h(\mathbf{u})]\)。

为了计算\(\mathbb{E}_{u}[h(\mathbf{u})]\)，我们将\(h(\mathbf{u})\)实现为缩放的点积注意力。

我们将\(U\)近似为一个固定的混杂字典 \(\mathbf{D}{u}=\left[\mathbf{u}{1}, \mathbf{u}{2}, \ldots, \mathbf{u}{N}\right] \in \mathbb{R}^{N \times d_{u}}\) ，其中\(N\)为单词类别数，\(d_u\)为隐藏特征维数。那么，我们有

\[\mathbb{E}{u}[h(\mathbf{u})]=\sum{u}\left[\operatorname{softmax}\left(\frac{\mathbf{Q}^{T} \mathbf{K}}{\sqrt{d{m}}}\right) \odot \mathbf{D}{u}\right] P(\mathbf{u}) \tag{13} \]

其中，\(\mathbf{Q}=\mathbf{W}{q} \mathbf{t}, \mathbf{K}=\mathbf{W}{k} \mathbf{D}{u}\)（\(\mathbf{W}{q}\)和\(\mathbf{W}_{k}\)是可学习的权重参数），\(d_m\)表示比例因子，\(P(\mathbf{u})\)表示先验统计概率，\(⊙\)是元素积。

用反事实推理减轻图像偏见

上一节已经成功去除了心理语言偏见，但虚假新闻检测模型中仍然存在图像偏见。

为了减轻仅图像的偏见，我们提出了反事实推理，通过阻止\(T\)和\(C\)的影响来估计\(I\)对\(Y\)的直接因果效应。

图©显示了假新闻检测的反事实世界的因果图，它描述了当\(I\)被设置为不同值\(i\)和\(i^∗\)时的场景。我们也将\(T\)设为它的参考值\(t^∗\)，因此当\(T = t^∗\)且\(I = i^∗\)时，\(C\)将获得值\(c^∗\)。这样，\(T\)和\(C\)的输入被阻塞，模型只能依靠给定的图像\(i\)进行检测。于是，我们可以得到\(I\)对\(Y\)的自然直接效应(NDE)，即图像偏置：

\[\mathrm{NDE}=Y{t^{}, i, c^{}}-Y{t^{}, i^{}, c^{*}} \tag{14} \]

此外，可以通过从总效应TE中减去NDE来消除偏置：

\[\mathrm{TIE}=\mathrm{TE}-\mathrm{NDE}=Y{t, i, c}-Y{t^{}, i, c^{}} \tag{15} \]

TIE是我们用于推理的去偏结果。

训练与推理

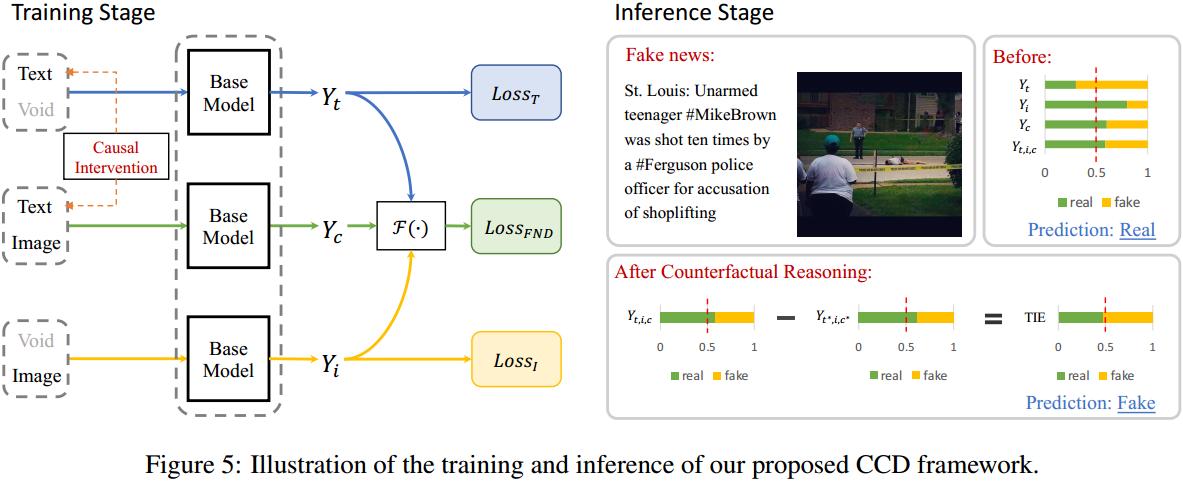
本图说明了我们提出的CCD框架的训练和推理。

对于训练阶段，我们计算每个分支的损失，包括基础多模态假新闻检测分支(\(Loss_{FND}\)），纯文本检测分支(\(loss_T\))和纯图像检测分支(\(Loss_I\))。
因此，我们最小化了一个多任务训练目标来学习模型参数，其公式为：

\[\operatorname{Loss}=\operatorname{Loss}{F N D}+\alpha \operatorname{Loss}{T}+\beta \operatorname{Loss}_{I} \tag{16} \]

其中\(Loss{FND}\)是指与公式(7)中\(\mathcal{F}(Y{t}, Y{i}, Y{c})\)预测相关的交叉熵损失。纯文本和纯图像损失\(loss_T\)和\(Loss_I\)是与\(Y_t\)和\(Y_i\)预测相关的交叉熵损失。\(α\)和\(β\)是权衡超参数。

在推理阶段，我们使用去偏效应进行推理，其实现为：

\[\begin{align} \mathrm{TIE} & =Y{t, i, c}-Y{t^{}, i, c^{}} \tag{17} \
& =\mathcal{F}\left(Y{t}, Y{i}, Y{c}\right)-\mathcal{F}\left(Y{t^{}}, Y{i}, Y{c^{}}\right) \tag{18} \end{align} \]