论文“Bi-directional Distribution Alignment for Transductive Zero-Shot Learning”提出Bi-VAEGAN，它以f-VAEGAN-D2为Baseline，进一步发展了TF- VAEGAN通过利用所见数据和反馈模块增强生成的视觉特征思路。f-VAEGAN-D2的介绍、TF-VAEGAN的介绍

引言

取决于标签是否可用，可以分为无条件分布\(p(v)\)或条件分布\(p(v|y)\)。当以辅助信息为条件时，可以学习辅助数据的联合分布。这种分布可以连接视觉空间与辅助知识，并引入生成器作为知识迁移的工具。通过适当的监督如条件鉴别器判断生成的图像是否是真实的野猫，将类内数据分布与真实数据分布保持一致。TZSL的难题在于转移可见类的分布，对未见类分布建模，实现未见类的真实生成。

实现这一问题的代表方法是f- VAEGAN：它使用了无条件判别器增强了未见类的生成，并学习未见类的数据分布。大多数现有工作在前向生成过程中使用辅助数据输出图像，即\(p(v|y)\)。这种使用条件的弱引导生成对辅助信息质量十分敏感。

为了实现视觉和辅助数据更好对其，增强与未见类的条件分布对齐，作者提出了一种新颖的双向生成过程。它将前向生成过程与后向生成过程结合起来，即通过 \(p(y|x)\) 从图像生成辅助数据。作者的工作基于f-VAEGAN，总体的改进包括：

1. 添加转导回归器以形成反向生成，以图像视觉特征为条件，生成伪辅助特征。这与 f-VAEGAN 中使用的前向生成一起，提供了更多约束来学习未见类的条件分布，实现视觉和辅助空间的更好对齐。
2. 引入L2特征归一化的数据预处理，帮助条件对齐。
3. 作者注意，未见类的先验分布对于分布对齐十分重要，尤其是不平衡数据集，先验的选择不当容易导致对齐不良。为了解决这个问题，作者提出了一种简单有效的类先验估计方法，该方法基于未见类别示例中包含的聚类结构。

方法

问题定义

使用\(V^s=\{{\bm v}_i^s\}^{ns}{i=1}\)和\(V^u=\{{\bm v}_i^u\}^{nu}{i=1}\)表示可见类与不可见类的示例，表示由预训练的网络提取的视觉特征。每一个可见类的label表示为：\(Y^s=\{y_i\}^{ns}{i=1}\)。以属性作为辅助信息，描述可见类和不可见类，用向量集表示：\(A^s=\{{\bm a}^s_i\}^{Ns}{i=1}\)和\(A^u=\{{\bm a}^u_i\}^{Nu}{i=1}\)。\(N_s\)和\(N_u\)分别表示可见类和未见类的类的数量。

在TZSL设置下，训练分类器\(f({\bm v}):\mathcal{V}^u\rightarrow\mathcal{Y}^u\)对未见类的数据进行推理，\(\mathcal{V}\)表示视觉特征空间，\(\mathcal{Y}\)表示标签空间。

整体训练的信息表示为：\(D^{tr}=\{\langle V^s,Y^s\rangle,\{A^s,A^u\},V^u,\}\)，这里\(\langle\cdot,\cdot\rangle\)表示配对数据。

L2特征归一化

特征归一化可以帮助模型训练收敛，一般的TZSL采用Min-Max 归一化\({\bm v}‘=\frac{{\bm v}-\min({\bm v})}{\max({\bm v})-\min({\bm v})}\)。然而作者提出了L2归一化的trick认为更有利，对于视觉特征向量\({\bm v}\in V^s\cup V^u\)：

\[{\bm v}’=L_2({\bm v},r)\frac{r{\bm v}}{|{\bm v}|_2} \tag{1} \]

其中超参数\(r>0\)为控制规划特征向量的范数。利用L2归一化层替换了生成器中伴随Min- Max方法的最后一个sigmoid层。作者在文中记录了L2与Min-Max归一化的曲线，L2归一化在早期训练中具有更高的精度和更快的收敛速度,比Min- Max表现更好。通过对比r大小设置，发现较小的r可能会导致性能更稳定,而较大的r会导致梯度增加，从而可能导致训练不稳定。

双向对齐模型

模型共有六个组成部分：

1. 条件VAE编码器：\({\bm E}:\mathcal{V}\times\mathcal{A}\rightarrow\mathbb{R}^k\)，在类别属性的条件下，将视觉特征映射到k维隐藏向量。
2. 条件视觉生成器：\({\bm G}:\mathcal{A}\times\mathbb{R}^k\rightarrow\mathcal{V}\)，在类别属性的条件下，从正态分布\(\mathcal{N}(0,1)\)中采样k维随机向量合成视觉特征。
3. 来自WGAN的条件视觉判别器：\(D:\mathcal{V}^s\times\mathcal{A}\rightarrow\mathbb{R}\)，处理可见类。
4. 来自WGAN的视觉判别器：\(D^u:\mathcal{V}^u\rightarrow\mathbb{R}\)，处理未见类。
5. 回归器：\({\bm R}:\mathcal{V}\rightarrow\mathcal{A}\)，将视觉空间映射到属性空间。
6. 来自WGAN的属性判别器：\(D^a:\mathcal{A}\rightarrow\mathbb{R}\)。

工作流分为两个Level：

• 在Level1，回归器\({\bm R}\)使用判别器\(D^a\)进行对抗训练，让视觉特征转换而来的伪属性与真实属性对齐。
• 在Level2，使用两个判别器\(D\)和\(D^u\)对抗训练视觉生成器\({\bm G}\)，让生成的视觉特征与真实的视觉特征对齐。

此外，G的训练取决于R。这鼓励用于合成视觉特征的伪属性要更好地与真实属性对齐。“双向对齐”正是得名于：在视觉和属性空间中对齐真伪数据。

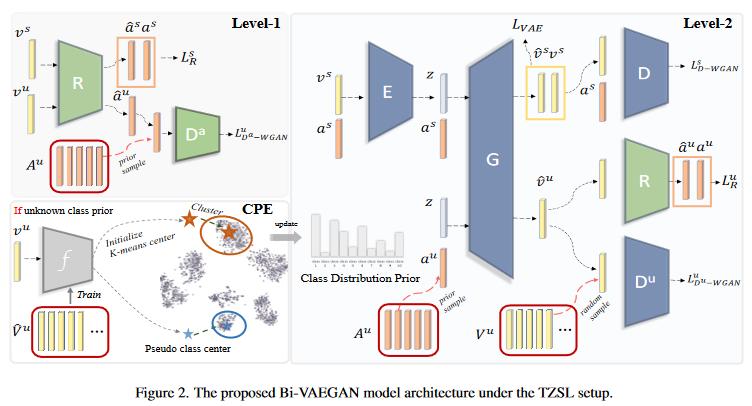
Level 1：回归器R训练

回归器\({\bm R}\)的训练具有转导性和对抗性。

• 对于可见类执行监督学习，实现视觉特征到属性特征的映射。
• 对于未见类的视觉特征和类属性进行无监督学习来增强（这里未见类的示例与特征是不配对的），学习未见类的整体特征分布。

\({\bm R}\)的学习通过最小化视觉特征的映射与其相应属性。

\[L^s_R(\mathcal{A}^s,\mathcal{V}^s)=\mathbb{E[\lVert\mathcal{R({\bm v}^s)-{\bm a}^s}\rVert_1]} \tag{2} \]

对于未见类，通过区分未见类的真实特征的真实属性\({\bm a}^u\)和真实特征计算的伪属性\(\hat{\bm a}^u\)，通过对抗学习实现。

\[L^u{D^a-WGAN}(\mathcal{A}^u,\mathcal{V}^u)=\mathbb{E}[D^a({\bm a}^u)]-\mathbb{E}[D^a(\hat{\bm a}^u)]+\mathbb{E}[(\lVert\nabla{\overline{\bm a}^u}D^a(\overline{\bm a}^u) \rVert_2-1)^2] \tag{3} \]

其中\(\hat{\bm a}^u={\bm R}({\bm v}^u),\ {\bm a}^u\sim p^u_{\bm G}(y),
\overline{\bm a}^u\sim \mathcal{P}t({\bm a}^u,\hat{\bm a}^u)\)，未见类的先验分布以\(p^u{\bm G}(y)\)表示，计算将在下文提到。原始属性从该先验分布采样的过程作者称为：先验采样过程。前两项计算了真实分布与模型分布的Earth- mover距离，等式的第三项为梯度惩罚，它实现了WGAN中的Lipschitz限制。

\(\mathcal{P}_t({\bm a},{\bm b})\)是L2超球面的插值分布。从该分布的采样计算为：\({\bm c}=L_2(t{\bm a}+(1-t){\bm b},r),\ t\sim\mathcal{U}(0,1),\ \lVert {\bm a}\rVert_2=\lVert {\bm b}\rVert_2=r\)

训练目标可定义为：

\[\min{\boldsymbol{R}}\max{D^a}~LR^s+\lambda L{D^a\text{-WGAN}}^u\tag{4} \]

其中\(\lambda\)为超参数。这使得知识分布在属性空间，未见类向可见类转移。然而特征的可辨别性受枢纽化问题的限制。但是也可以利用这一点，为后续，在视觉空间中进行分布对齐提供近似监督。

枢纽化问题（Hubness）是指在高维空间中，一些样本点成为了其他样本点的近邻枢纽，即在数据集中，存在一些数据点它们与大多数其他数据点具有更近的距离。

Level 2：生成器G和编码器E训练

回归器\({\bm G}\)的训练也具有转导性和对抗性，目的是对齐合成特征与真实特征。在属性空间上冻结\({\bm R}\)，视觉空间上使用判别器\(D\)和\(D^u(\hat{\bm v}^u)\)。

两个判别器需要经过训练，以区分真实的视觉特征和条件生成器计算的合成视觉特征。设\(\hat{\bm v}\sim G(\boldsymbol{a},\boldsymbol{z})\)，其中\({\boldsymbol{z}\sim\mathcal{N}}(\boldsymbol{0},\boldsymbol{1}),
\boldsymbol{a}\sim{p{\boldsymbol{G}}}(y)\)。对于可见类的先验分布定义为\(p{\boldsymbol{G}}^{s}(y)\)，该分布可以根据每个类的样本数简单估计得到。未见类的先验分布还是\(p_{\bm G}^u(y)\)。生成的视觉特征\(\hat{\bm v}\)已经通过G进行L2归一化。

• 对于可见。判别器以类属性为条件，即\(D(\hat{\bm v},{\bm a}^s)\)。

\[\begin{aligned} L{D-WGAN}^{s}(A^{s},V^{s})=& \mathbb{E}[D({\bm v}^s,{\bm a}^s)]-\mathbb{E}[D(\hat{\bm v}^s,{\bm a}^s)]+ \
&\mathbb{E}[(|\nabla{\bar{{\bm v}}^s}D(\bar{{\bm v}}^s,{\bm a}^s)|_2-1)^2] \end{aligned}\tag{5} \]

• 对于未见类判别器是无条件的，即\(D^u\)。

\[\begin{aligned} L{D^{u}-WGAN}^{u}(A^{u},V^{u})=& \mathbb{E}[D^u({\bm v}^u)]-\mathbb{E}[D^u(\hat{\bm v}^u)]+ \\ &\mathbb{E}[(|\nabla{\bar{{\bm v}}^u}D^u(\bar{{\bm v}}^u)|_2-1)^2] \end{aligned} \tag{6} \]

这里，\(\bar{\bm v}^s,\ \bar{\bm v}^u\)由插值分布中采样得到（参见上文）。这里\(\hat{\bm v}^u\)由从\({\bm a}^u\sim p^u_{\bm G}(y)\)采样的未见类属性计算得到。公式(5)、(6)弱对齐了未见类条件分布，但缺少监督。为了提高对齐健壮性，引入了另一个训练损失：

\[L_R^u(A^u)=\mathbb{E}[|R(G({\bm a}^u,{\bm z}))-a^u|_1] \tag{7} \]

这里使用Level 1训练的R来执行监督约束。这可以防止模型坍塌，并作为GAN训练的补充。相似的，还对VAE进行训练，以增强可见类的对抗训练：

\[\begin{aligned}L{VAE}^s(A^s,V^s)&=\mathbb{E}[\mathrm{KL}(E({\bm v}^s,{\bm a}^s)|\mathcal{N}(\mathbf{0},1))]+ \\ &\mathbb{E}{{\bm z}^s\sim{\bm E}({\bm v}^s,{\bm a}^s)}[(|G({\bm a}^s,{\bm z}^s)-{\bm v}^s|_2^2)]\end{aligned}\tag{8} \]

第一项为KL散度，第二项使用L2归一化特征重建均方差（Mean-squared-error, MSE）。最后，总的训练目标为：

\[\min{{\bm E},{\bm G}}\max{D,D^{u}}L{{VAE}}^{s}+\alpha L{D-{WGAN}}^{s}+\beta L{R}^{u}+\gamma L{D^{u}-{WGAN}}^{u} \tag{9} \]

这里，\(\alpha,\ \beta,
\gamma\)为超参数。训练包括了已知类的成对的视觉特征和未见类的估计类分布，通过R进行监督增强，以进一步约束未见类的视觉特征生成。

提出的Bi-VAEGAN可通过移除\(V^u\)，以适应归纳ZSL：

\[\begin{aligned}&\text{For level-1:}\min{\boldsymbol{R}}L{R}^{s}\&\text{For level-2:}\min{\boldsymbol{E},\boldsymbol{G}}\max{D}L{{VAE}}^{s}+\alpha L{D\cdot{WGAN}}^{s}+\beta L_{R}^{u}\end{aligned}\tag{10} \]

未见类先验估计

公式(3)(6)中提到，未见类属性采样\({\bm a}^u\sim p{{\bm G}}^u(y)\)。由于没有标签信息，无法从真实的类先验中采样\(p^u(y)\)。作者发现，由于骨干网络，未见类的样本在视觉空间中具有直观的集群结构。作者采用K- means聚类，重点设计聚类中心的初始化。估计的先验分布\(p{{\bm G}}^u(y)\)迭代更新，并在每个epoch，根据额外的分类器\(f\)计算的伪类中心重新初始化。对于第一次初始化，使用归纳训练的生成器来转移可见类的配对知识，以便对未见类更好估计。这种估计称为聚类先验估计（the cluster prior estimation, CPR），实现过程如1-12行所示（给它翻译了下）：

模型预测和特征增强

完成6个模块的训练后，将训练未见类的样本分类模型\(f:\mathcal{V}^{u}(\mathrm{or}\hat{\mathcal{V}}^u)\times\mathcal{H}^u\times\hat{\mathcal{A}}^u\to\mathcal{Y}^{u}\)。使用的特征向量\({\bm x}^u=[{\bm v}^u,{\bm h}^u, \hat{\bm a}^u]\)由三部分组成：\({\bm v}^u ({\rm or}
\hat{\bm v}^u)\)表示视觉特征，\(\hat{{\bm a}}^{u}=\boldsymbol{R}\left({\bm v}^{u}\right)\)表示回归器计算的伪属性，\({\bm h}^u\)由回归器第一个全连接层返回。它集成了生成器和回归器的知识，具有更强的区分性。

参考文献

1. Wang, Zhicai, et al. “Bi-directional Distribution Alignment for Transductive Zero-Shot Learning.” Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2023.