[概率论与数理统计]笔记：4.3 常用的统计分布

4.3 常用的统计分布

上侧分位数

分位数是一个分界点。

上侧分位数与分布函数 \(F\)以及水平 \(\alpha\)有关，常记为\(F_\alpha\).

含义 ：

在\(y=F(x)\)的图像中，使得直线\(x=F\alpha\)右侧区域 积分面积等于 \(\alpha\)的\(F\alpha\)就是上侧分位数 。

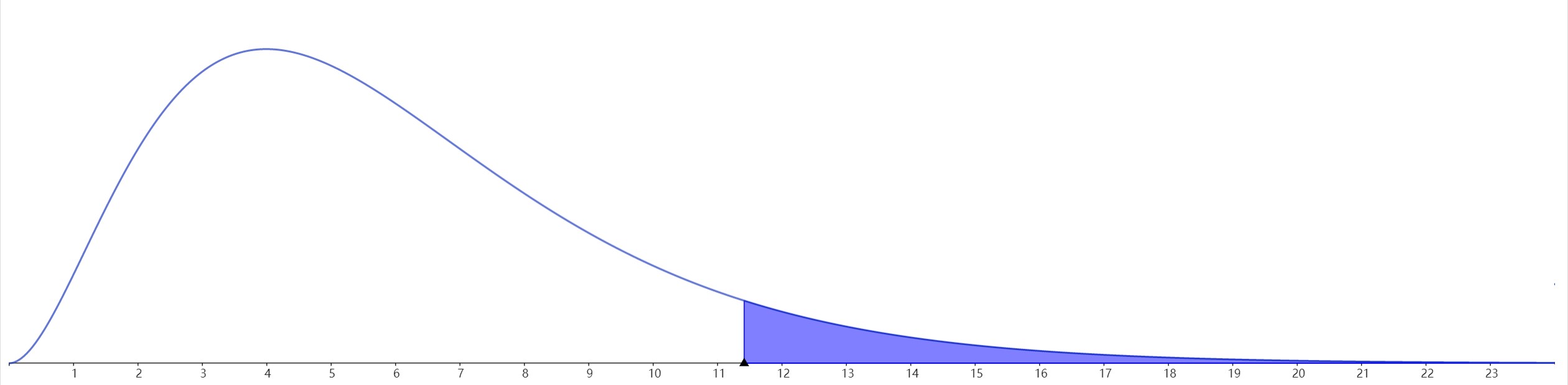
常见表述：\(P\{X>F_\alpha\}=\alpha\)

也就是找出使得右侧面积等于\(\alpha\)的分界点\(F\alpha\)，计算非常复杂，一般都是通过查表得到\(F\alpha\).

---

\(\chi ^2\)分布

如果\(X_1,\cdots,X_n\)独立，且\(Xi\sim N(0,1)\)，那么\(\sum\limits{i=1}^nXi^2\)服从\(\chi^2\) 分布，记作\(\sum\limits{i=1}^nX_i^2\sim \chi^2(n)\). 其中\(n\)称为自由度 。

• \(EX=n\)
• \(DX=2n\)

如果\(X\sim \chi^2(n)\)，当\(n\)充分大时，\(\frac{X-n}{\sqrt{2n}}\)近似服从 \(N(0,1)\)，即标准正态分布。

可加性

如果\(X\sim \chi^2(m),Y\sim\chi^2(n)\)，\(X,Y\)独立，则\(X+Y\sim\chi^2(m+n)\).

推论

如果\(X_i\sim\chi^2(mi)\)且独立，其中\(1\le i\le n\)，则\(\sum\limits{i=1}^nXi\sim\chi^2(\sum\limits{i=1}^nm_i)\).

---

t分布

\(X\sim t(n)\)

• 当\(n\)很小，\(t\)分布与正态分布区别很大。
• 当\(n\ge30\)时，\(t\)分布与正态分布的区别不大。

定义

如果\(X\sim N(0,1),Y\sim \chi^2(n)\)且\(X,Y\)独立，则\(\frac{X}{\sqrt{Y/n}}\sim t(n)\).

\(t\)分布关于\(y\)轴对称，因此其上侧分位数有性质：

\[t{1-\alpha}(n)=-t\alpha(n) \]

---

F分布

\(X\sim F(n_1,n_2)\)

定义

如果\(X\sim \chi^2(n_1),Y\sim \chi^2(n_2)\)且\(X,Y\)独立，则\(\frac{X/n_1}{Y/n_2}\sim F(n_1,n_2)\).

推论

如果\(X\sim F(n_1,n_2)\)，那么\(\frac{1}{X}\sim F(n_2,n_1)\).

上侧分位数有性质：

\[F_{1-\alpha}(n_1,n2)=\frac{1}{F\alpha(n_2,n_1)} \]

使用教材：
《概率论与数理统计》第四版 中国人民大学 龙永红 主编 高等教育出版社