[概率论与数理统计]笔记：3.5 大数定律与中心极限定理

3.5 大数定律与中心极限定理

切比雪夫不等式

定义

\(EX\)和\(DX\)存在，对于任意的\(\epsilon>0\)，有

\[P\{|X-EX|\ge\epsilon\}\le \frac{DX}{\epsilon^2} \]

证明

这里证明\(X\)是连续型的情况。

\[\begin{align} 左边 &= \int\limits{|X-EX|\ge\epsilon}f(x)\mathrm{d}x \
&\le \int\limits{|X-EX|\ge\epsilon}\frac{(X-EX)^2}{\epsilon^2}f(x)\mathrm{d}x \\ &\le \int{-\infty}^{+\infty}\frac{(X-EX)^2}{\epsilon^2}f(x)\mathrm{d}x \\ &= \frac{1}{\epsilon^2}\int{-\infty}^{+\infty}(X-EX)^2f(x)\mathrm{d}x\
&= \frac{DX}{\epsilon^2}=右边 \end{align} \]

因此，\(P\{|X-EX|\ge\epsilon\}\le \frac{DX}{\epsilon^2}\).

证明过程补充说明 ：

第一个不等号是因为\(|X-EX|\ge\epsilon\)，两边平方，就有\((X-EX)^2\ge\epsilon^2\)，于是\(\frac{(X-EX)^2}{\epsilon^2}\ge1\)，因此乘上这个系数就会大于等于原来的积分。

第二个不等号是因为积分区域扩大了，并且被积函数是密度函数是非负的 ，所以有大于等于的不等关系。

最后的定积分化为方差，其实就是连续型随机变量的方差计算公式。👉随机变量的方差-计算-连续型

理解

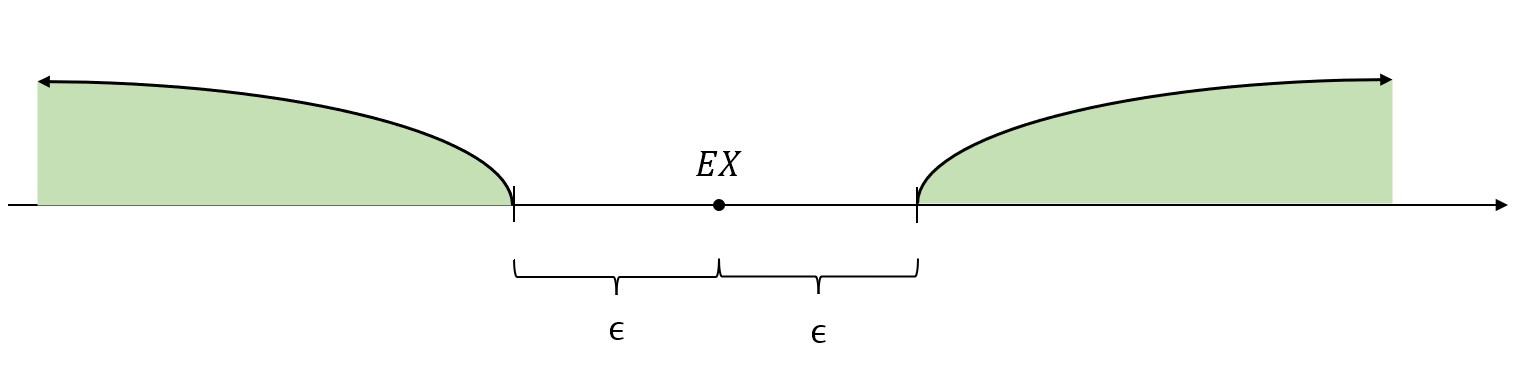
\(|X-EX|\)可以理解为随机取一个点，这个点到\(EX\)的距离。

那么\(P\{|X-EX|\ge \epsilon\}\)，就表示随机取一个点，这个点到\(EX\)的距离大于指定的\(\epsilon\)的概率。也就是上图中随机取的点落在绿色区域的概率。

\(EX\)是\(X\)的“中心点”，\(X\)的取值大多数都围绕在\(EX\)不远处。因此，落在“外面”的点是比较少的，落在“外面”的概率是比较小的，并且通过上面的放缩证明，这个概率是小于\(\frac{DX}{\epsilon^2}\)的。

• \(DX\)越小，说明数据的整体波动较小，说明数据都集中分布在\(EX\)附近，那么落在“外面”的概率就小。
• \(DX\)越大，说明数据的整体波动较大，说明数据分布比较分散，那么落在“外面”的概率就比较大。
• \(\epsilon\)越小，说明划定的“内部区域”比较小，那么落在“外面”的概率就比较大。
• \(\epsilon\)越大，说明划定的“内部区域”比较大，那么很多点都被包含在“内部”了，落在“外面”的点就变少了，所以落在“外面”的概率也就比较小。

可以看出，概率大小与\(DX\)的正相关关系以及和\(\epsilon\)的负相关关系是和切比雪夫不等式吻合的。

推论

切比雪夫不等式为

\[P\{|X-EX|\ge\epsilon\}\le \frac{DX}{\epsilon^2} \]

将切比雪夫不等式的范围取反，则可以得到

\[P\{|X-EX|<\epsilon\}\ge1-\frac{DX}{\epsilon^2} \]

---

依概率收敛

收敛

如果\(a_n\to a\)，要求\(\forall \epsilon>0,\exists N>0,n>N时,|a_n-a|<\epsilon\).

理解 ：对于任意\(\epsilon>0\)在于划定一个非常小的区域，\(\exists N>0\)在于存在某一项，\(n>N\)也就是说这一项后面的所有项\(a_n\)，与一个数\(a\)的距离都要小于先前划定的非常小的\(\epsilon\)，也就是说\(a_n\to a\).

依概率收敛

对于任意\(\epsilon>0\)，有

\[\lim\limits_{n\to\infty}P\{|X_n-X|>\epsilon\}=0 \]

则称\(\{X_n\}\) 依概率收敛到\(X\)，记作\(Xn\stackrel{P}{\longrightarrow}X\)或\(P-\lim\limits{n\to\infty}X_n=X\).

理解 ：依概率收敛没有上面的收敛那么严格，它并不要求当\(n>N\)时，\(|X_n-X|<\epsilon\)恒成立。只是要求当\(n\)足够大时，\(|X_n-X|<\epsilon\)的概率为1。从数轴上理解就是：前者要求\(n>N\)的所有数都落在狭小的范围内，而依概率收敛只要求最终的概率为1，可以偶尔有几个点是落在狭小区域外面 。

---

大数定律

在\(n\)次试验中事件\(A\)发生的次数记为\(\mu_n\)，发生的频率为\(\frac{\mu_n}{n}\)。\(\mu_n\) 和\(\frac{\mu_n}{n}\)都是随机变量。

伯努利大数定律

定理

\(n\)重伯努利试验中，事件\(A\)发生了\(\mu_n\)次，频率为\(\frac{\mu_n}{n}\)，频率依概率收敛 于事件\(A\)发生的概率\(p\).

\[\lim\limits_{n\to\infty}P\{|\frac{\mun}{n}-p|<\epsilon\}=1 \
\lim\limits{n\to\infty}P\{|\frac{\mu_n}{n}-p|\ge\epsilon\}=0 \]

证明

因为\(\mu_n\sim B(n,p)\)，

所以

\[\begin{align} & E(\mu_n)=np \\ & D(\mu_n)=np(1-p) \end{align} \]

\(n\)为常数，结合数学期望和方差的相关性质，有

\[\begin{align} & E(\frac{\mu_n}{n})=p \\ & D(\frac{\mu_n}{n})=\frac{p(1-p)}{n} \end{align} \]

根据切比雪夫不等式（对应的随机变量\(X\)是\(\frac{\mu_n}{n}\)），对于任意\(\epsilon>0\)，有

\[P\{|\frac{\mu_n}{n}-p|<\epsilon\}\ge1-\frac{\frac{p(1-p)}{n}}{\epsilon^2}\tag{*} \]

不等式右边

\[1-\frac{\frac{p(1-p)}{n}}{\epsilon^2}=1-\frac{p(1-p)}{n\epsilon^2} \]

当\(n\to\infty\)时，\(上式\to1\).

又根据概率的基本性质，\(P\{|\frac{\mu_n}{n}-p|<\epsilon\}\le1\).

所以，\((*)\)式可延伸为

\[1\ge P\{|\frac{\mu_n}{n}-p|<\epsilon\}\ge1-\frac{\frac{p(1-p)}{n}}{\epsilon^2}\to1 \]

根据夹逼定理，

\[P\{|\frac{\mu_n}{n}-p|<\epsilon\}=1 \]

所以

\[P\{|\frac{\mu_n}{n}-p|\ge\epsilon\}=0 \]

结论

当\(n\to\infty\)时，\(\frac{\mu_n}{n}\stackrel{P}{\longrightarrow}p\).

也就是说当试验次数很多时，事件发生的频率会依概率收敛 于事件发生的概率。

---

切比雪夫大数定律

定理

\(X_1,X_2,\cdots,X_n,\cdots\)是一系列不相关 的随机变量，\(EX_i\)和\(DX_i\)均存在，方差有界，即\(DX_i\le M\).

对于任意\(\epsilon>0\)，有

\[\lim\limits{n\to\infty}P\{|\frac{1}{n}\sum\limits{i=1}^nXi-\frac{1}{n}\sum\limits{i=1}^nEX_i|<\epsilon\}=1 \]

证明

\[E(\frac{1}{n}\sum\limits_{i=1}^nXi)=\frac{1}{n}\sum\limits{i=1}^nEX_i \]

\(X_1,\cdots,X_n,\cdots\)不相关，所以\(cov(X_i,X_j)=0\).

\[D(\frac{1}{n}\sum_{i=1}^nXi)=\frac{1}{n^2}\sum\limits{i=1}^nDX_i\le\frac{nM}{n^2}=\frac{M}{n} \]

根据切比雪夫不等式（对应的随机变量\(X\)是\(\frac{1}{n}\sum\limits_{i=1}^nX_i\)），有

\[P\{|\frac{1}{n}\sum\limits_{i=1}^nXi-\frac{1}{n}\sum\limits{i=1}^nEXi|<\epsilon\}\ge1-\frac{D(\frac{1}{n}\sum\limits{i=1}^nX_i)}{\epsilon^2} \]

这里的\(D(\frac{1}{n}\sum\limits_{i=1}^nXi)\)前面有负号，所以上式中的\(D(\frac{1}{n}\sum\limits{i=1}^nX_i)\le\frac{M}{n}\)中的不等符号在这里要转换：

\[P\{|\frac{1}{n}\sum\limits_{i=1}^nXi-\frac{1}{n}\sum\limits{i=1}^nEXi|<\epsilon\}\ge1-\frac{D(\frac{1}{n}\sum\limits{i=1}^nX_i)}{\epsilon^2}\ge1-\frac{M}{n\epsilon^2} \]

当\(n\to\infty\)时，有

\[1\ge P\{|\frac{1}{n}\sum\limits_{i=1}^nXi-\frac{1}{n}\sum\limits{i=1}^nEX_i|<\epsilon\}\ge1-\frac{M}{n\epsilon^2}\to1 \]

根据夹逼定理，

\[P\{|\frac{1}{n}\sum\limits_{i=1}^nXi-\frac{1}{n}\sum\limits{i=1}^nEX_i|<\epsilon\}=1 \]

推论

如果\(X_1,\cdots,X_n,\cdots\)独立同分布 ，其数学期望和方差都存在，这些随机变量的期望都是\(EX_i=\mu\).

对于任意的\(\epsilon>0\)，有

\[\lim\limits{n\to\infty}P\{|\frac{1}{n}\sum\limits{i=1}^nX_i-\mu|<\epsilon\}=1 \]

---

辛钦大数定律

定理

如果\(X_1,\cdots,X_n,\cdots\)独立同分布 ，随机变量的期望都是\(EX_i=\mu\)，方差无要求。

对于任意的\(\epsilon>0\)，有

\[\lim\limits{n\to\infty}P\{|\frac{1}{n}\sum\limits{i=1}^nX_i-\mu|<\epsilon\}=1 \]

结论

这个定理说明了当试验次数很大时，可以用数据的平均值来估计期望值。

案例

测桌子长度：在测量的过程中误差是无法避免的，那么可以多次测量求平均值 ，并且用该平均值来估计期望值（桌子的实际长度）。

---

中心极限定理

大量独立同分布 的变量之和的极限分布是正态分布 。

林德伯格-列维中心极限定理

\(X_1,\cdots,X_n,\cdots\)独立同分布(不管什么分布都行)，\(EX_i=\mu,DX_i=\sigma^2\)，\(0<\sigma^2<+\infty\)。

\[\lim\limits{n\to\infty}P \left\{ \frac{\sum\limits{i=1}^nX_i-n\mu}{\sqrt{n}\sigma} \le x \right\} =\varPhi_0(x) \]

大量独立同分布的变量之和标准化之后的极限分布就是标准正态分布。

补充说明

设变量之和为\(Y=\sum\limits_{i=1}^nXi\)，则\(EY=E\sum\limits{i=1}^nXi=n\mu,DY=D(\sum\limits{i=1}^nXi)=\sum\limits{i=1}^nDX_i=n\sigma^2\).

变量之和标准化之后：

\[Y^*=\frac{Y-EY}{\sqrt{DY}}=\frac{\sum\limits_{i=1}^nX_i-n\mu}{\sqrt{n}\sigma} \]

---

棣莫弗-拉普拉斯中心极限定理

\(Y_n\sim B(n,p)\)

\[\lim\limits_{n\to\infty}P\{\frac{Y_n-np}{\sqrt{np(1-p)}}\le x\}=\varPhi_0(x) \]

其中

\[Yn=\sum\limits{i=1}^nX_i,\quad X_i= \left\{ \begin{align} & 1, 发生\\ & 0,未发生\\ \end{align} \right. \]

\(EX_i=p,\ DX_i=p(1-p)\)

也就是说只要把林德伯格-列维中心极限定理 中的数学期望和方差进行替换，就可以得到棣莫弗-拉普拉斯中心极限定理.

结论 ：二项分布可以用正态分布去近似。

当\(n\)较大时，二项分布的计算量是非常大的。

而正态分布的计算可以查表。

---

补充

• 当\(n\)大，\(np\)适中时，将二项分布 近似为泊松分布 。
• 当\(n\)大，\(np\)大时，将二项分布 近似为正态分布 。

参考值 ：

• 泊松分布对应的\(n\)的较大值大概为：80，100，200左右。
• 正态分布对应的\(n\)的较大值一般为：几千几万。

使用教材：
《概率论与数理统计》第四版 中国人民大学 龙永红 主编 高等教育出版社