VAE 学习笔记

VAE 是 AE的变体。主要目的是让模型学习数据的分布，最后让解码器(decoder)部分具有生成样本的能力。
VAE可看做高斯混合模型(GMM)的扩展。
GMM中，数据由多个高斯分布来描述:

\[p(x) = \sum{k=1}^{K}P(z{k})P(x|z_{k}) \]

其中 \(z \sim P(z^{k}) \), \(x|z^{k} \sim N(\mu^{k}, \sigma^{k})\)
此处，高斯分布的数量是有限的。

因此，这种编码方式编码能力有限。因此需要对这种方式拓展为连续编码。

\[p(x) = \int_{z} p(x|z)p(z)d z \]

其中 \(z\sim N(0,1), x|z \sim N(\mu (z), \sigma (z))\).

求解方式是最大化似然:

\[\max L = \sum_{x} \log p(x) \]

我们引入\(q(z|x)\)， 它可以是任意一个概率分布。做如下等价变化。

\[\begin{align} \log p(x) & = \int{z}q(z|x)\log p(x) dz \\ & = \int{z}q(z|x)\log \frac{p(z, x)}{p(z|x)} dz \\ & = \int{z}q(z|x)\log \left(\frac{p(z,x)}{q(z|x)} \frac{q(z| x)}{p(z|x)}\right) dz \\ & = \int{z}q(z|x)\log \left(\frac{p(z,x)}{q(z|x)} \right) dz + \int{z}q(z|x) \left(\frac{q(z| x)}{p(z|x)}\right) dz \\ & = \int{z}q(z|x)\log \left(\frac{p(z,x)}{q(z|x)} \right) dz + KL(q(z| x)||p(z|x)) \\ & \geq \int_{z}q(z|x)\log \left(\frac{p(z,x)}{q(z|x)} \right) dz \end{align} \]

也即是

\[\log p(x) \geq \int_{z}q(z|x)\log \left(\frac{p(z,x)}{q(z|x)} \right) dz \]

我们定义

\[L{b} = \int{z}q(z|x)\log \left(\frac{p(z,x)}{q(z|x)} \right) dz \]

优化目标变为了同时优化\(q(z|x)\) 和 \(p(z|x)\)。

如果仅仅优化\(q(z|x)\), 由于\(\log p(x)\) 与\(q(z|x)\) 无关，那么 \(\log p(x)\) 不变化，它仅仅会增大\(L{b}\), 因此，也缩小了KL. 如果KL缩小为0， 那么调节KL就会增大\(\log p(x)\). 而且最后，因为KL的缩小，最后的 \(q(z|x)\) 可以近似 \(p(z|x)\).

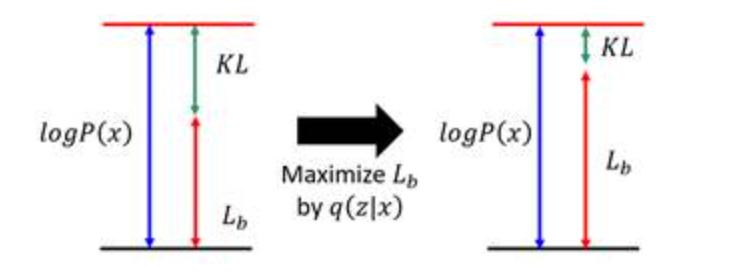
对于\(L{b}\),我们作进一步分解。

\[\begin{align} L{b} &= \int{z}q(z|x)\log \left(\frac{p(x|z) p(z )}{q(z|x)} \right) dz \\ &= \int{z}q(z|x)\log p(x|z) dz + \int{z} q(z|x) \log \frac{p(z)}{q(z|x)} dz \\ &= -KL(q(z|x)||p(z)) + \int_{z}q(z|x)\log p(x|z) dz \end{align} \]

第一项展开如下（可参考VAE原文附录）：

\[\sum{i=1}^{l}(\exp(\sigma{i}) - (1 + \sigma{i}) + (m{i})^{2}) \]

对于第二项，

\[\begin{align} & \max \int{z}q(z|x)\log p(x|z) dz \\ & = \max E{q(z|x)}[\log p(x|z)] \end{align} \]

这里其实就是auto-encoder的损失。
参考:
李宏毅机器学习 https://www.bilibili.com/video/av15889450/?p=33
https://www.gwylab.com/note-vae.html