Q-REG

2023-09-27 airxiv preprint

Jin, S., Barath, D., Pollefeys, M., & Armeni, I. (2023). Q-REG: End-to-End Trainable Point Cloud Registration with Surface Curvature.

• paper: 2309.16023v1] Q-REG: End-to-End Trainable Point Cloud Registration with Surface Curvature (arxiv.org)
• code: waiting

Questions Raised

1. RANSAC-like estimation methods cope with the combinatorics of the problem via selecting random subsets of m correspondences( e.g., m=3 for rigid pose estimation). this allows to progressively explore the \((\frac{n}{m})\) possible combinations, where n is the total number of matches.

简单来说就是RANSAC style不可微，不能end-to-end；而其他learning-based方法为了实现端到端就将hard correspondence换成了基于socre的soft correspondence(hard就是True or False，soft就是有权重，或者说点对匹配程度)，又会使得计算开销太大，并且引入大量噪声。

作者就想实现hard correspondence的端到端，怎么办，采用single correspondence来预测变换就可以了，这样就没有random subsets，而是迭代遍历correspondence set，取最好预测结果。

Contribution

1. 设计了Q-REG，一种结合single correspondence的local surface patches(fitting quadrics)，来估计位姿的点云配准方法，意图替代RANSAC。从介绍上，Q-REG与correspondence matching method 无关(it is agnostic to the correspondence matching method)，并且能够快速做outlier rejection by filtering degenerate solutions and assumption inconsistent motions (rigid poses inconsistent with motion priors (e.g., to avoid unrealistically large scaling).)
2. 将Q-REG设计成可微(differentiable)方案，用于无论是在correspondence matching method 还是 pose estimation method的端到端训练
3. 刷SOTA哩

Description

employing higher-order geometric information , Q-REG achieving exhaustive search to replace RANSAC and improve the performance and run-time

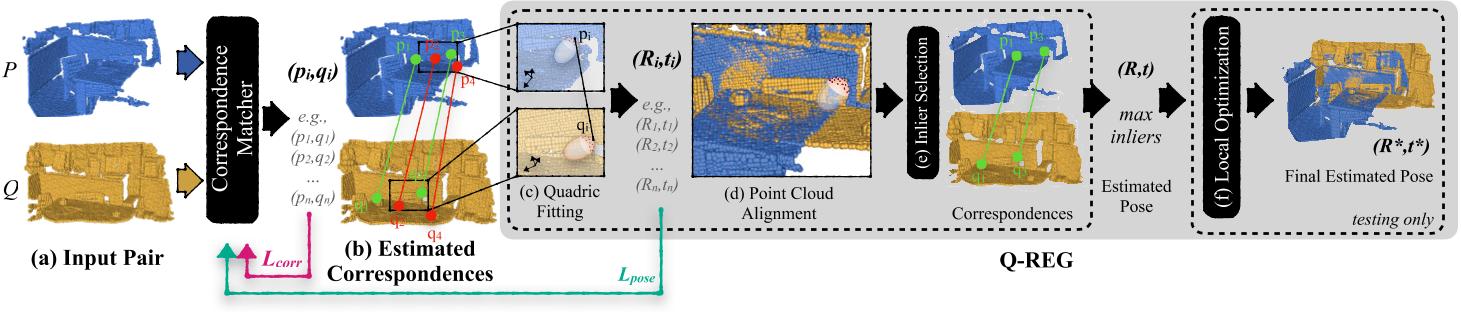
First Step: Correspondence Matching

使用任意Correspondence Matcher（e.g patch-based: PPFNet, PPF-FoldNet; full-conv: FCGF）得到feature-matching based putative correspondences \(\{P, Q\}\in C\) , 用于之后的Q-REG方法预估变换矩阵。

Q-REG是single-correspondence方法，因此区别于RANSAC每次随机挑选三对corresponding point \(\{p, q\}\) 预测变换矩阵，Q-REG每次只取单对corresponding point，用于estimate transform between \(P\) and \(Q\) 。

Second Step: Q-REG

Q-REG直接当作工具用的步骤为：

1. 从correspondence set \(C\) 中迭代取出single correspondence \(\{p,\ q \}\) ;
2. 对以每个single corrspondence为输入预测变换矩阵
3. 选择best transformation model 作为初步结果, the pose quality metric is calculated as the cardinality of its support i.e., the number of inliers.
4. 之后根据论文[^ 1] 的方法进行local optimization.( a local re-sampling and re-fitting of inlier correspondences based on their normals (coming from the fitted quadrics) and positions. )

如果嵌入端到端训练则只进行到第二步时根据预测结果构建Loss: \(L_{pose}\) 。

后文对single correspondence为输入预测变换矩阵的过程进行详述，以及介绍 \(L_{pose}\) 的构成

1. Quadric Fitting based local patch

对于single correspondence \(\{p, q\}\in C\) ，可以为点划分local patch(Q-REG通过K=50的KNN来划分)，预测一对local patch，并计算两个loca patch彼此的LRF(local reference frame) \(R_p, R_q \in SO(3)\) （即作为将点从世界坐标系转换到局部参考系的旋转矩阵）。假如预测正确，我们就可以做两片点云的对齐( \(R=R_qR_p^T\) )。因此Q- REG应用二次曲面拟合来预估 \(R_p,\ R_q\) 。

至于translation vector \(t\) ，论文直接以 q, p作为两片点云重叠区域的质心， \(t=q-p\) 。

论文中应用如下约束拟合3D quadric surface：

\[\hat{p}^TQp=0 \]

• \(\hat{p}\) ：3D homogeneous point(3D齐次点) lying on the surface
• Q is the quadirc parameters in matrix as:

\[Q = \begin{pmatrix}A&D&E&G\\D&B&F&H\\E&F&C&I\\G&H&I&J\end{pmatrix} \]

理论上最佳的是local patch的所有点都能落在曲面上，但是当然不可能🤗，所以需要拟合。

之后，作者重写了上述公式便于应用：

• \(|\mathcal{N}|\) is the number of neighbors to which the quadric is fitted(paper sets to 50). 换句话说，二次曲面拟合不用single corrspondence 中的p，q点，也就是keypoints，而是使用local patch中的其他点，也就是neighbor points.
• \(d_i\) 是第i个neighbor point离原点(the origin)的平方距离(squared dist)。（所以这里实现时是不是需要先对local patch以keypoint求相对距离进行标准化）。

使用上述linear equation获得 \(Q\) 中的系数。

然后对求得二次曲面系数矩阵 \(Q\) 应用平移，使得keypoint能落在曲面上，也就是调整系数 \(J\) 使得对于keypoint，公式 \(p^TQp =0\) 成立。

最终取二次曲面系数矩阵 \(Q\) 的部分，得到如下矩阵 \(P\) ，并使用对矩阵 \(P\) 使用 Eigen-decomposition ，得到特征向量矩阵 \(V\) 作为求得LRF \(R_p或R_q\) 。

注意：为了保留尺度(scaling) 信息，这里不对特征向量进行单位化。

2. Estimate rigid Transformation

the rotation \(R=R_pPR_q^T \in SO(3)\) ，其中 \(P\) 表示一个unknown permutation matrix，用于控制p的LRF与q的LRF之间的各轴对应关系，这种对应关系分三种情况考虑：

1. 当LRF三轴的模（长度）各不相同时，也就是x-y-z三方向尺度信息都不一致。只需要按照三轴的长度从大到小排列对应即可 。这种方式基于这样的假设：该过程建立在点云中没有或有但是可忽略的各向异性缩放的假设之上，因此相对应轴长度保持不变。这种方式可以实现scale-invariant，并且通过不可实现的缩放过滤不可靠匹配。因此，rigid transformation可以通过single correspondence解决。
2. 当LRF三轴的模（长度）其中两个相同，与另一个不相同时，也就是x-y-z三方向有两个方向尺度信息一致，那么直观上就可以理解：两个方向尺度信息一致，使得一对一匹配LRF三轴时，有两对轴无法明确匹配。因此，需要最起码two correspondences来互相印证，保证 \(P\) 矩阵预测正确。
3. 当LRF三轴的模（长度）都相同，也就是x-y-z三方向尺度都一致，此时local patch以keypoint为原点接近一个sphere surface。同理，需要最起码three correspondences。

所以为了实现estimate rigid transformation from a single correspondence，只保留 \(C\) LRF三轴的模（长度）各不相同的corrspondences，各轴长度差都大于 \(10^{-3}\) 。之后就可以用 \(R=R_pPR_q^T\) 公式计算刚性旋转矩阵。

3. End-to-End Training Loss

\[\epsilon (T{p,q}) = \sqrt{\frac{1}{|C|}\sum{(p_i,qi) \in C}{||T{p,q}p_i-q_i}||_2^2} \]

\[L{pose} = \sum{(p,q)\in C}{(1-\frac{min(\epsilon(T_{p,q}), \gamma)}{\gamma} -s)} \]

• \(\gamma\) is a threshold and \(s\) is the score of the point correspondence predicted by the matching network

上述所提到的 \(L_{pose}\) 可以与其他广泛使用的registration loss functions 相结合实现从特征匹配到配准的端到端训练。

Experiments

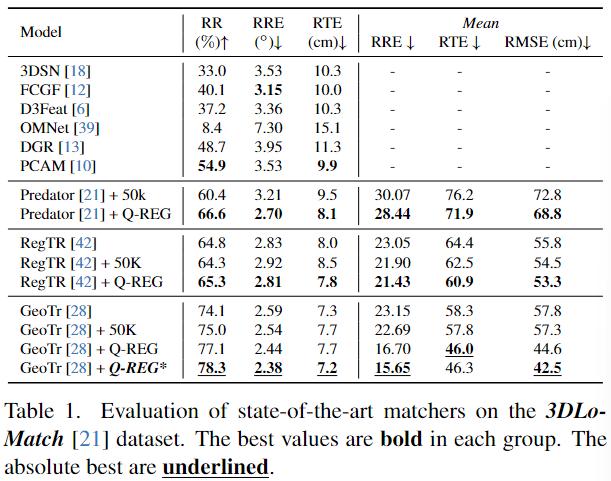
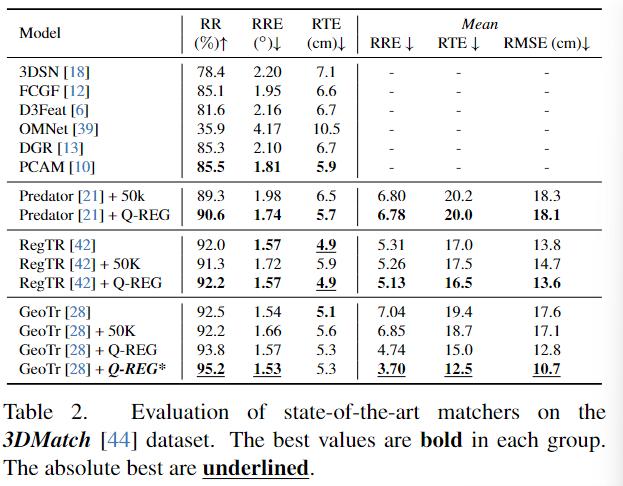
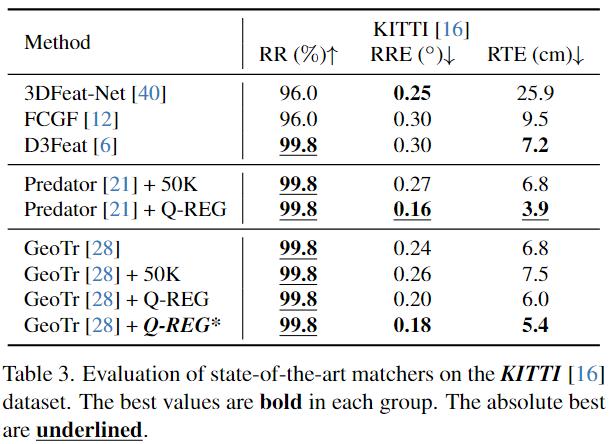
1. dataset：3DMatch、3DLoMatch；KITTI；ModelNet、ModelLoNet
2. corresponding matcher：Predator、RegTR、GeoTr
3. metrics：RR(registration recall)、RRE(registration rotation Error)、RTE(Registration Translation Error)、

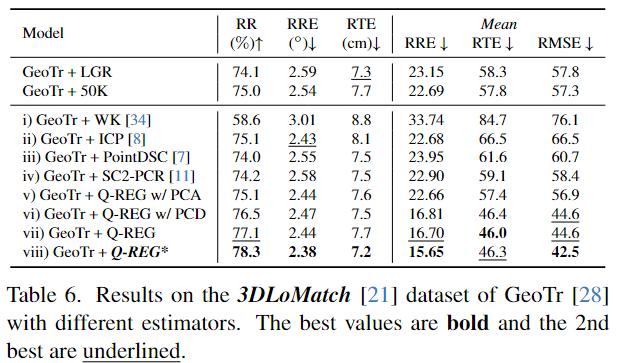
没说的，在matcher一致的情况下全SOTA，并且还比其他estimator(ICP、PointDesc……)好.消融实验也证明了Q- REG所有component都有效提升了一定的指标额度：quadric-fitting single-corresponding solver、local optimation、used in end-to-end training。

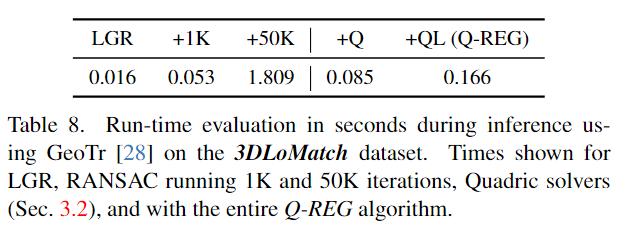
Run-time

[^ 1]:Karel Lebeda, Jirı Matas, and Ondrej Chum. Fixing the locally optimized ransac-full experimental evaluation. In British machine vision conference. Citeseer, 2012. 5